(V) 高次トポロジカル絶縁体の物理

トポロジカル絶縁体は近年発見された物性物理における重要な概念です。 最近では物性物理に留まらず量子情報・素粒子分野などでも関心を集めています。 トポロジカル絶縁体には、バルクは絶縁体ですが，サンプルの境界にギャップレスな状態が現れます。 これはバルクにゼロではないトポロジカル数が定義されているためであり，バルク境界対応と呼ばれています。これは、サンプルの外は真空なのでトポロジカル数はゼロです。 一方、トポロジカル数は量子化しており，ギャップが閉じない限り変化できません。 故に，サンプル内部と真空の境界でギャップが閉じなければなりません。 この結果，$D$次元のトポロジカル絶縁体には$D-1$次元のギャップレス境界状態が現れます。 このように、トポロジカル絶縁体の表面状態の存在はトポロジカルに保護されているので、ランダムさや不純物に対してロバストであり、デバイスの微細化・高性能化・エラー耐性化に寄与すると考えられています．同様の議論は超伝導体にも適用でき、トポロジカル超伝導体と呼ばれています。 最近、このトポロジカル絶縁体を拡張した高次トポロジカル絶縁体という概念が提出され着目を浴びています。 例えば、３次元トポロジカル絶縁体には２次元表面状態が現れます。しかし、３次元２次トポロジカル絶縁体の表面状態にはギャップがありますが，結晶の稜線には１次元状のギャップレスなヒンジ（hinge）状態が現れます。 同様に２次元トポロジカル絶縁体には１次元のエッジ状態が現れます。一方、２次元２次トポロジカル絶縁体ではエッジ状態にはギャップがありますが、試料のコーナーには０次元状のゼロエネルギー・コーナー状態が現れます。 これらの現象は、明らかに従来のトポロジカル絶縁体固有のバルク境界対応と異なっています。

★ Breathing カゴメ格子での高次トポロジカル絶縁体★

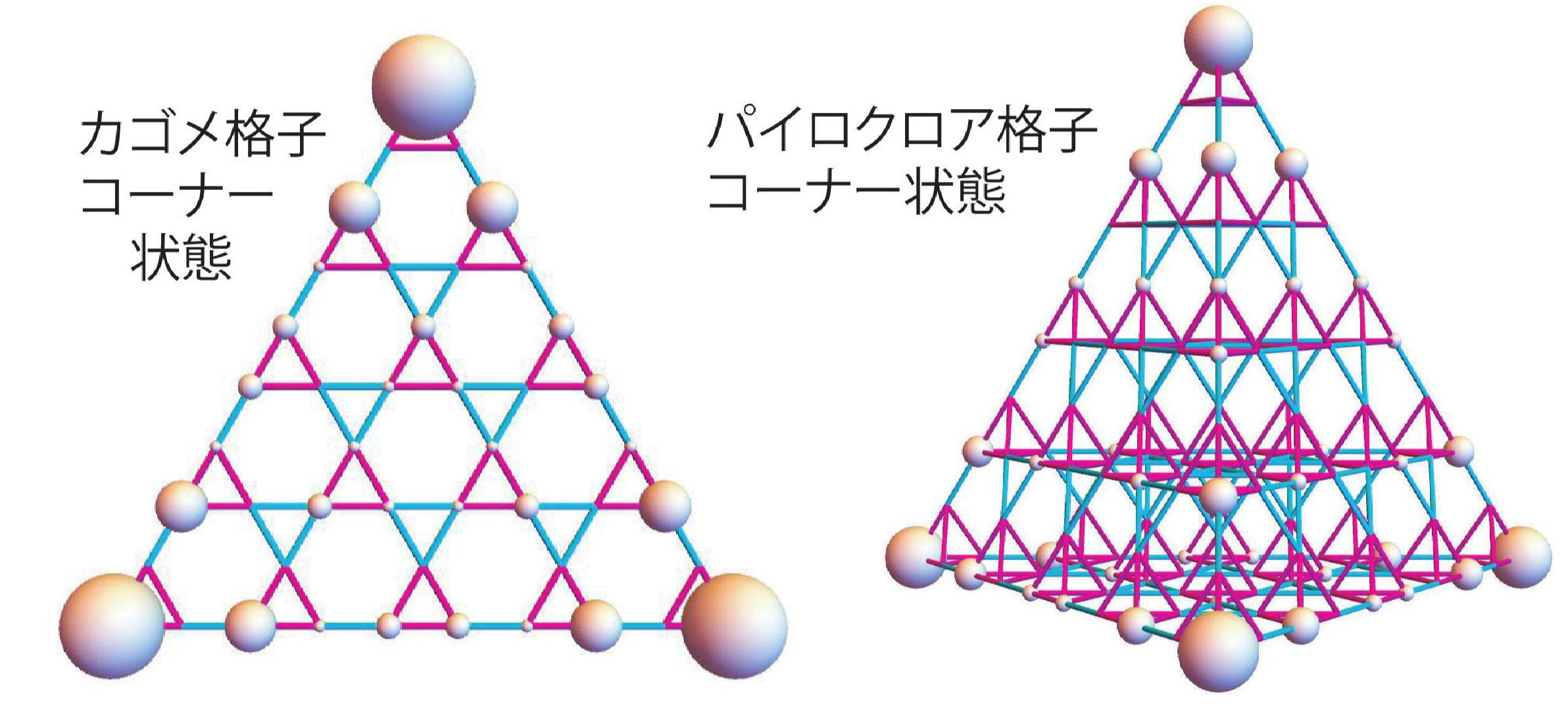
カゴメ格子で高次トポロジカル絶縁体を実現する方法を提案しました[PRL120, 026801 (2018) ]。通常のトポロジカル絶縁体は二次元ではエッジ状態を持ちますが、二次トポロジカル絶縁体にはエッジ状態はなく、０次元のコーナー状態を持ちます。 本研究ではSSH模型をカゴメ格子上に拡張する事で二次トポロジカル相を実現しました。従来から提案されていた模型は正方格子上でのみ定義されていましたが、この研究により、正方格子以外の系でも普遍的に高次トポロジカル相が実現する事が確立しました。 従来の模型と異なり、この模型ではホッピング・パラメータの符号が同じなので実験的にも実現が容易です。実際、この理論提案は音響格子系で独立に二つのグループにより検証され、ともにNature Materials[1,2]に掲載されています。また、固体表面上に分子を吸着する事によりSTMで観測がされ、これもNature Materials[3]に掲載されています。この現象に関して、Nature Materialsの依頼で、同誌に「News & Views」の執筆を行いました[4]。光学格子でも観測されました[5,6]。また、LC電気回路においてもカゴメ格子二次トポロジカル相が実現する事を予言しました[PRB98, 201402(R) (2018) ]。これは実験で実現しました[7]。 更に、パイロクロア格子で三次トポロジカル絶縁体が実現する事も予言しましたが、 これも音響系で実現しました[8,9]。
[1] H. Xue, Y. Yang, F. Gao, Y. Chong and B.Zhang, "Acoustic higher-order topological insulator on a kagome lattice" Nature Materials 18, 108 (2019).
[2] X. Ni, M. Weiner, A. Alu and A. B. Khanikaev, "Observation of higher-order topological acoustic states protected by generalized chiral symmetry" Nature Materials 18, 113 (2019).
[3] S. N. Kempkes, M. R. Slot, J. J.van den Broeke, P. Capiod, W.A. Benalcazar, D.Vanmaekelbergh, D. Bercioux, I. Swart, C. Morais Smith, "Robust zero-energy modes in an electronic higher-order topological insulator: the dimerized Kagome lattice" Nature Materials 18, 1292 (2019)
[4] M. Ezawa, "Protected corners", Nature Materials, News & Views,18, 1266 (2019).
[5] A. E. Hassan, F. K. Kunst, A. Moritz, G. Andler, E. J. Bergholtz, M. Bourennane, "Corner states of light in photonic waveguides" Nature Photonics 13, 697 (2019)
[6] M. Li, D. Zhirihin, D. Filonov, X. Ni, A. Slobozhanyuk, A. Alu and A. B. Khanikaev, "Higher-order topological states in photonic kagome crystals with long-range interactions" Nature Photonics 14, 89 (2020)
[7] J. Wu, X. Huang, J. Lu, Y. Wu, W. Deng, F. Li, and Z. Liu, "Observation of corner states in second-order topological electric circuits" Phys. Rev. B 102, 104109 (2020)
[8] M. Weiner, X. Ni, M. Li, A. Alu, A. B. Khanikaev, "Demonstration of a 3rd order hierarchy of higher order topological states in a three-dimensional acoustic metamaterial" Science Advances 27 Mar 2020: Vol. 6, no. 13, eaay4166
[9] H. Xue, Y. Yang, G. Liu, F. Gao, Y. Chong and B. Zhang, "Realization of an Acoustic Third-Order Topological Insulator", Phys. Rev. Lett. 122, 244301 (2019).