Generalized braids and their presentations
We consider various presentations for the generalizations of braids. Here we give two
examples.
In his initial paper on braids E. Artin gave a presentation of an arbitrary braid
group with two generators. The analogous presentation for the complex braid group
B(2e,e,r) have the generators τ2,τ, σ,τ2
′ and relations
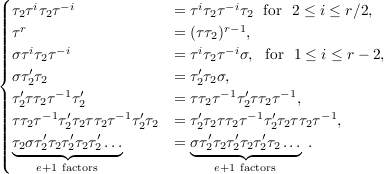
In the second example we give an analogue of the Sergiescu graph presentation.
Theorem 1. Let Γ be a planar graph with n vertices. The singular braid monoid
SBn has the presentation 〈XΓ,RΓ〉where XΓ = {σa,σa
-1, xa ∣ a is an edge of Γ}
and RΓ is formed by the following six types of relations:
- disjointedness: if the edges a and b are disjoint, then
- commutativity:
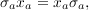
- invertibility:
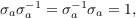
- adjacency: if the edges a and b have a common vertex, then
- nodal: if the edges a, b and c have a common vertex and are placed clockwise,
then
- pseudocycle: if the edges a1, …, an form an irreducible pseudocycle and if
a1 is not the starting edge nor an is the end edge of a reverse, then
