Thermal quantum states
[Iwaki-Hotta, arXiv:2202.07207 (2022), Iwaki-Shimizu-Hotta, PRR (2021)]
熱的量子状態. これは有限温度の熱平衡にある量子状態のことをさします. 統計力学にはCanonical typicality という考え方があります. かのJ. von Neumann, Z. Phys. 57, 30 (1929) がはじめて言及した発想で, [Popescu, Short, Winter, NaturePhys. 2, 754 (2006).“ で定式化されて同時期にGoldstein, et.al. PRL 96, 050403 (2006) から名前がついています]: 熱力学的には同じ局所物理量を期待値として持つ状態は「無数」にあって, どれか1個がたまたま実現したとして他の状態と特にマクロな局所物理量を見る限り区別がつくわけではない, という捉え方です. だからensemble physicsは古い(?)から脱却するぞ, というニュアンスの主張が2006年の論文でなされています. たしかにそのとおりで, このような捉え方はもっと昔から物性物理の数値計算屋さんたちは気づいていた わけですがよりはっきり市民権を得るようになったのは上記の論文のあとくらいではないかと思います.
基底状態には通常, 純粋状態としてのuniqueな表現(等価なものはあってよい)しか存在しませんので, 質的に異なったいくつもの状態が同じ状態を指す事象は有限温度 熱平衡状態ならではのことです.
では, 現実にあるサイズNの系の量子状態を作ろうとしたとき どのような選択肢があるでしょうか? 量子状態には純粋状態と混合状態があります(see 青本 Sec 3.2). 純粋状態とは1つのケットで量子状態の情報が完備された状態で, 混合状態とは系の量子力学的な状態について完全な情報を知るためにいくつものケットの和を要する状態です. これらは純粋度P=tr(ρ2);ではかることができます. 密度演算子ρは ボルツマン因子を演算子化したもので, 状態のケットとブラを背中あわせにしてできています.
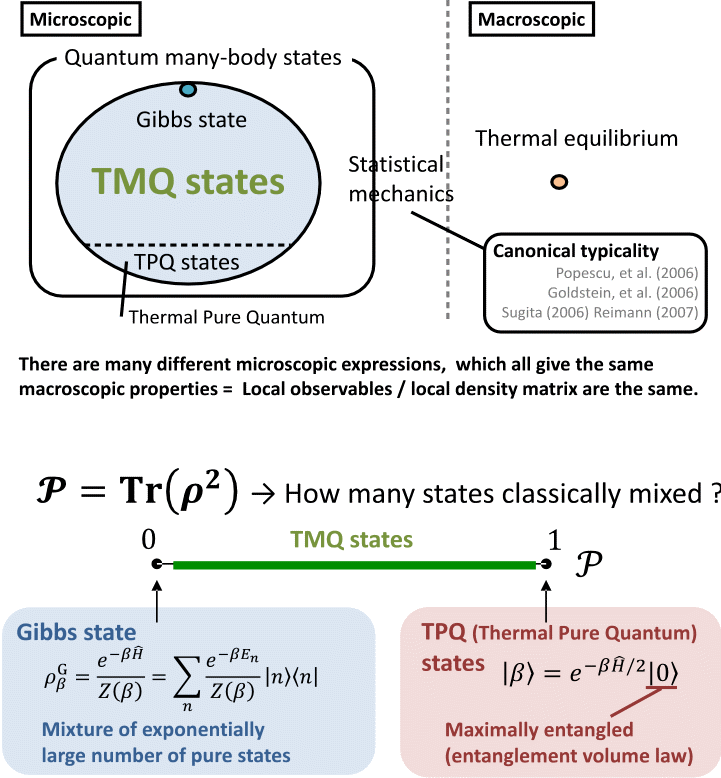
ある熱的な状態が与えられたとき その純粋度が1の場合, Thermal pure quantum state(TPQ状態) ともよばれ
実際に ランダムな要素を持つ初期状態に対して e-βH/2を演算する(これを虚時間発展という)
ことによってつくることができます.
等価なミクロカノニカルな TPQ状態に関しては (l-H/N)を何回もかけることで簡便につくることができます [Sugiura-Shimizu PRL108, 240401(2012)].
その対極として Gibbs状態は expの数の量子状態の和として定義されており, 所謂, 統計力学のアンサンブル平均をまじめに取る操作に相当するため, その純粋度はexp(-N)のオーダーでゼロになります.
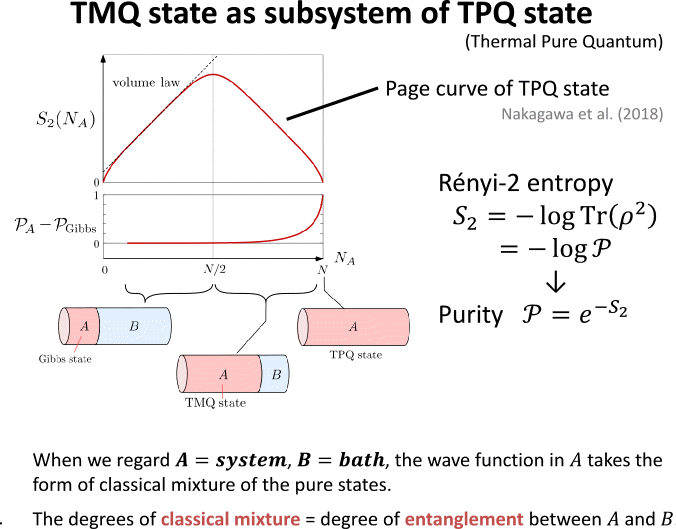
この二つの状態の間にある熱的量子状態を熱的混合状態 Thermal mixed quantum state(TMQ state) と呼ぶことにします. 直感的にTMQ状態がどう純粋度で特徴づけられているかを考えるために, ある一つの孤立系で実現される純粋状態を考えてそれをAとBに分割します. ここでAとBの間はエンタングルしていて其のエンタングルメントは, 部分密度行列ρAによって求められます. このような全孤立系を二つに分割したときのRenyi2エントロピーS2と呼ばれるエンタングルメントエントロピーは Page曲線に載ることが知られていて, さらにこのS2は部分系Aの波動関数の純粋度 PA のログで表されます. このことを利用すると部分系Aの純粋度PA は部分系Aのサイズが 半分より小さければ Gibbs状態と等価な小さな値をとりますが, Aが系の半分より大きくなると徐々に PA が上昇し, 最終的にAが全系となったときにPA=1となります. (論文のintroductionに解説してありますのでよかったらご参考ください.)
このことは次のように読み替えられます. 部分系Aが BとエンタングルするエントロピーがちょうどAだけに着目して混合状態ととらえたときの混合度で稼げるエントロピーと等価になっています. そのため Aが半分より小さいときには, A内で保持されているエンタングルメントは小さく, そのトレードオフとしてBをくっつけて purifyするのに十分なエンタングルメントが用意されています. ところがAが半分より大きくなるとA内で状態が強くエンタングルし合うようになり, かわりにBとのエンタングルメントは減っていきます. このように一般に 系の量子的なエンタングルメントがもたらすエントロピーは系の古典和(混合)がもたらす古典的なエントロピーと質的に異なったものではなく, 系の熱力学的エントロピーを量子エンタングルメントに振り分けるか古典混合に振り分けるかには任意性があります. もしAのエンタングルメントがその熱的状態のエントロピーを表現するのに不十分であれば それを補足するための古典混合を取らねばなりません.
その対極として Gibbs状態は expの数の量子状態の和として定義されており, 所謂, 統計力学のアンサンブル平均をまじめに取る操作に相当するため, その純粋度はexp(-N)のオーダーでゼロになります.
この二つの状態の間にある熱的量子状態を熱的混合状態 Thermal mixed quantum state(TMQ state) と呼ぶことにします. 直感的にTMQ状態がどう純粋度で特徴づけられているかを考えるために, ある一つの孤立系で実現される純粋状態を考えてそれをAとBに分割します. ここでAとBの間はエンタングルしていて其のエンタングルメントは, 部分密度行列ρAによって求められます. このような全孤立系を二つに分割したときのRenyi2エントロピーS2と呼ばれるエンタングルメントエントロピーは Page曲線に載ることが知られていて, さらにこのS2は部分系Aの波動関数の純粋度 PA のログで表されます. このことを利用すると部分系Aの純粋度PA は部分系Aのサイズが 半分より小さければ Gibbs状態と等価な小さな値をとりますが, Aが系の半分より大きくなると徐々に PA が上昇し, 最終的にAが全系となったときにPA=1となります. (論文のintroductionに解説してありますのでよかったらご参考ください.)
このことは次のように読み替えられます. 部分系Aが BとエンタングルするエントロピーがちょうどAだけに着目して混合状態ととらえたときの混合度で稼げるエントロピーと等価になっています. そのため Aが半分より小さいときには, A内で保持されているエンタングルメントは小さく, そのトレードオフとしてBをくっつけて purifyするのに十分なエンタングルメントが用意されています. ところがAが半分より大きくなるとA内で状態が強くエンタングルし合うようになり, かわりにBとのエンタングルメントは減っていきます. このように一般に 系の量子的なエンタングルメントがもたらすエントロピーは系の古典和(混合)がもたらす古典的なエントロピーと質的に異なったものではなく, 系の熱力学的エントロピーを量子エンタングルメントに振り分けるか古典混合に振り分けるかには任意性があります. もしAのエンタングルメントがその熱的状態のエントロピーを表現するのに不十分であれば それを補足するための古典混合を取らねばなりません.
Iwaki論文では, ランダムサンプリング法と呼ばれる古くから広く使われている考え方で構築された熱的な量子状態に対して, 必要な混合度 あるいは サンプル数をどのように形而上的に導き出すか?という疑問に対して定式化を与えています.
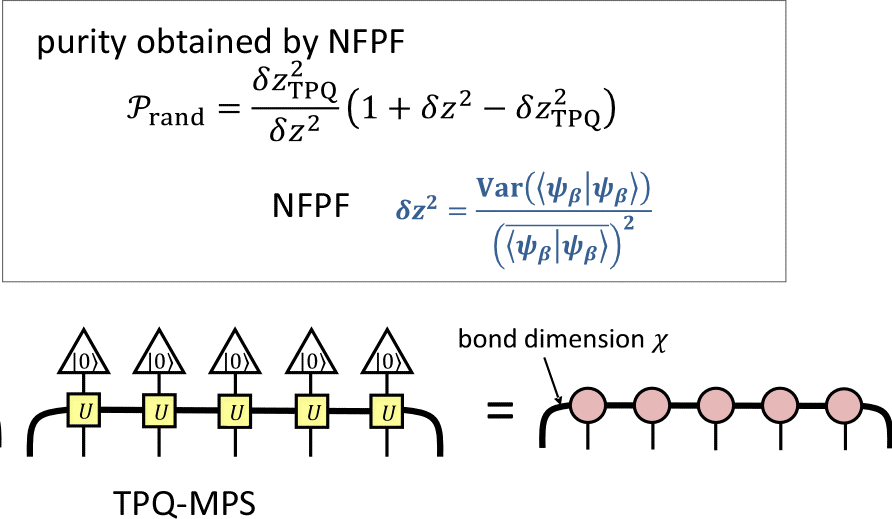
ランダムサンプリング法とは, 次のような枠組みです: 一般にある初期状態|0>を用意してそれに虚時間発展をほどこすと |ψ>=e-βH/2|0> という波動関数が得られます. この波動関数をつかった物理量Aの期待値は< X >=<ψ|X|ψ>/<ψ|ψ>= <0| e-βH X |0>/ <ψ|ψ> のようになりますが, ひとつの |ψ>だけでTPQ状態を成すような場合を除けば, これでは熱平衡状態の期待値を成しません. というのが特別に注意深く|0> を用意できた時以外には それほど質が良い(十分エンタングルメントを保持した)|ψ>を得ることは難しいからです. そこでM個の独立な状態に対して虚時間発展して得られた|ψj> について< X >thermal= Σ<ψj|X|ψj>/Z, という期待値をとればもしサンプル数Mが|ψj>の質(エンタングルメント)に比して十分な古典混合の数を成していれば, よいということになります. ここで 虚時間発展は非ユニタリなので, 得られた波動関数のノルムは1ではなく, またサンプルによってばらつきがあります. このばらついたノルムの平均値が 分配関数 Z=Σ<ψj|ψj>/M, です. そしてそのばらつき(揺らぎ)には物理的な意味があることがわかってきました.
Iwaki理論では, このノルムの揺らぎNFPF(normalized fluctuation of partition function)が, ちょうど必要とするサンプル数に比例しており, このNFPFを用いれば 系の純粋度も直接計算できるということを示しました.
ここでなぜこんなたくさんのサンプルを取ったり不確かな初期状態から虚時間発展をしてわざわざ質的に悪い熱平衡状態を創るようなシチュエーションを考えるの?という疑問も, たとえば量子情報的な視点では出てくると思います. しかし一般には私たち固体物性研究者は, 相互作用も量子効果もある大自由度(Nがおおきい)量子多体系を考えているわけです. Nが30くらいでTPQ状態はほぼ厳密にもとまりますが それ以上を超えるとまず数値的にはむつかしくなります. いろいろな近似をつかったり波動関数の形式を工夫したりしながら何とか質の良い 熱的な状態を作るにはどうするか? そしてその評価をどうやるか?という答えをNFPFが与えています.
もう少し一般的には, この理論やNFPFという量の意味合いは, 決してTMQ状態に限ったものではありません. ある特定の分布関数(ボルツマン分布以外)に従う量子多体波動関数を考えたとき その分布に対応してどのような量子混合状態がつくられその 純粋度がどう測定できるか?に関して全く同様の定式化が成り立ちます.
ランダムサンプリング法とは, 次のような枠組みです: 一般にある初期状態|0>を用意してそれに虚時間発展をほどこすと |ψ>=e-βH/2|0> という波動関数が得られます. この波動関数をつかった物理量Aの期待値は< X >=<ψ|X|ψ>/<ψ|ψ>= <0| e-βH X |0>/ <ψ|ψ> のようになりますが, ひとつの |ψ>だけでTPQ状態を成すような場合を除けば, これでは熱平衡状態の期待値を成しません. というのが特別に注意深く|0> を用意できた時以外には それほど質が良い(十分エンタングルメントを保持した)|ψ>を得ることは難しいからです. そこでM個の独立な状態に対して虚時間発展して得られた|ψj> について< X >thermal= Σ<ψj|X|ψj>/Z, という期待値をとればもしサンプル数Mが|ψj>の質(エンタングルメント)に比して十分な古典混合の数を成していれば, よいということになります. ここで 虚時間発展は非ユニタリなので, 得られた波動関数のノルムは1ではなく, またサンプルによってばらつきがあります. このばらついたノルムの平均値が 分配関数 Z=Σ<ψj|ψj>/M, です. そしてそのばらつき(揺らぎ)には物理的な意味があることがわかってきました.
Iwaki理論では, このノルムの揺らぎNFPF(normalized fluctuation of partition function)が, ちょうど必要とするサンプル数に比例しており, このNFPFを用いれば 系の純粋度も直接計算できるということを示しました.
ここでなぜこんなたくさんのサンプルを取ったり不確かな初期状態から虚時間発展をしてわざわざ質的に悪い熱平衡状態を創るようなシチュエーションを考えるの?という疑問も, たとえば量子情報的な視点では出てくると思います. しかし一般には私たち固体物性研究者は, 相互作用も量子効果もある大自由度(Nがおおきい)量子多体系を考えているわけです. Nが30くらいでTPQ状態はほぼ厳密にもとまりますが それ以上を超えるとまず数値的にはむつかしくなります. いろいろな近似をつかったり波動関数の形式を工夫したりしながら何とか質の良い 熱的な状態を作るにはどうするか? そしてその評価をどうやるか?という答えをNFPFが与えています.
もう少し一般的には, この理論やNFPFという量の意味合いは, 決してTMQ状態に限ったものではありません. ある特定の分布関数(ボルツマン分布以外)に従う量子多体波動関数を考えたとき その分布に対応してどのような量子混合状態がつくられその 純粋度がどう測定できるか?に関して全く同様の定式化が成り立ちます.
では本当にNが大きな系のTPQ状態かそれに準ずる状態は構成が困難なのか?という疑問に対しては
TPQ-MPSという行列積(MPS)状態を用いた記述を考えました.
通常のMPS波動関数(1次元)は一般に area law entanglementをもつ, つまり 系を2つにわったとき保持できる
エンタングルメント量が定数で頭打ちになるので page curveがすぐ破綻してしまいがちになります.
このような状況でも MPSの両端に auxiliaryというエンタングルメント浴をつけてやるだけで劇的に熱的な状態の質を向上させ, 系の端から端までvolume lawに従って長さに比例するエンタングルメントを保持させることに成功しています. このTPQ-MPSの計算は爆速でとても軽くて簡単です.
制度上は多少コントロールが必要ですが, ざっくり計算をするにはとても便利な方法です.