Spin orbit coupling induced exotic band structures
[Nakai, Hotta Nature Comm. 13, 579 (2022), Nakai-Kawano-Hotta, arXiv:2208.07171 (2022)]
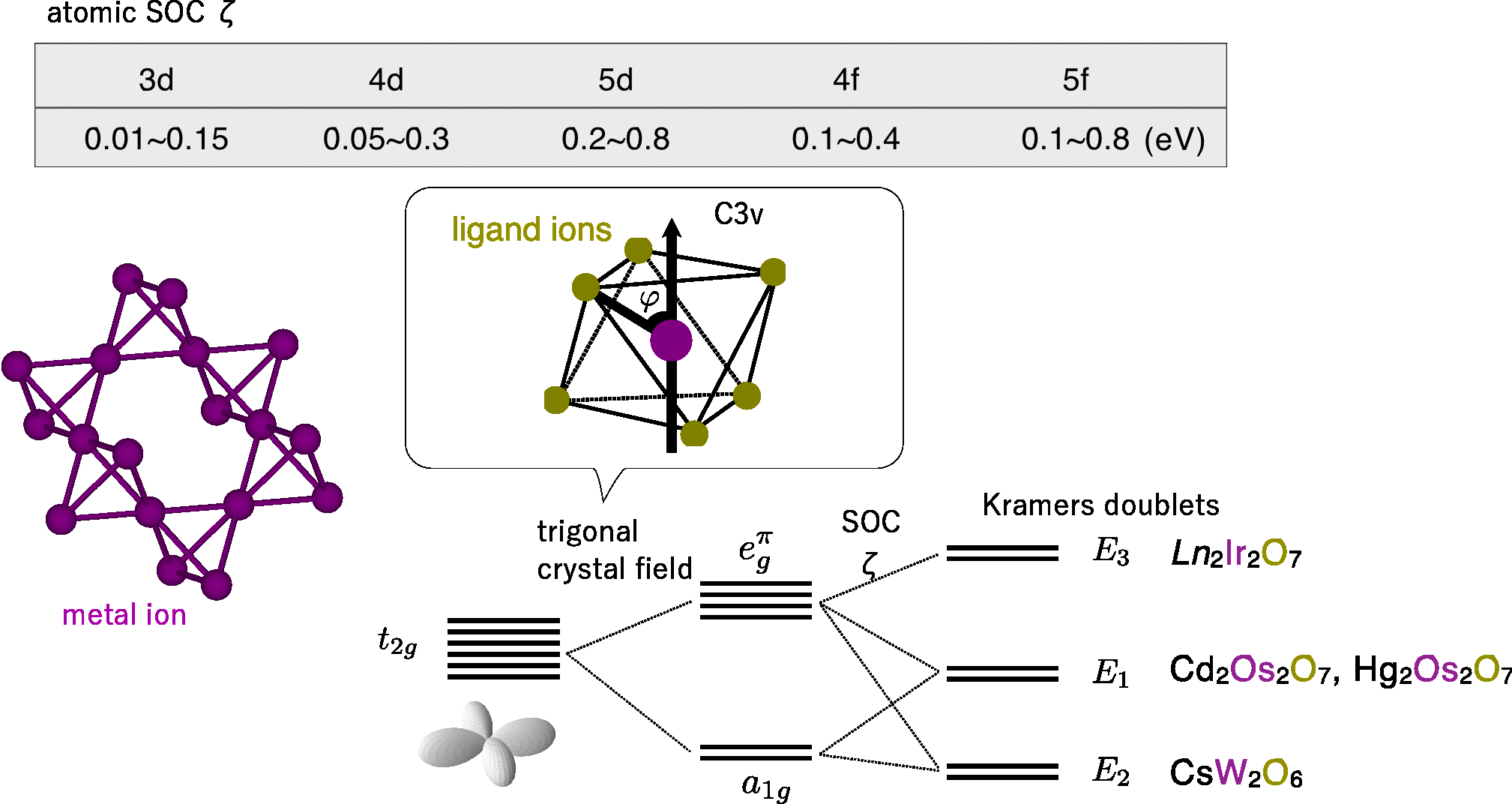
3d-5fまでの原子のスピン軌道相互作用(SOC)は表のように比較的強く、同時に3d-5dの電子は局在性が中庸なため, SOC電子系（金属も絶縁体も含む）が実現します. これらの電子系では、各原子の電子軌道は結晶場とSOCの影響で分裂します, たとえば3回対称な結晶場での 5d電子系の場合を示したものが図の通りです. t2g軌道がKramers二重項３つに分裂します. このうちの１つに電子１個入っているようなfillingを考えると ハミルトニアンとして 別ページにも示したような H_kin が最もシンプルなものとなります. このようなハミルトニアンがパイロクロア格子やカゴメ格子のようなフラストレート格子上の電子系で実現 している場合を以下では取り上げます. これらの格子では通常は反転対称性が保たれており、バンドは全てスピンに関して Kramers縮退をしています. （spin orbit coupled Mott insulatorの項参照）



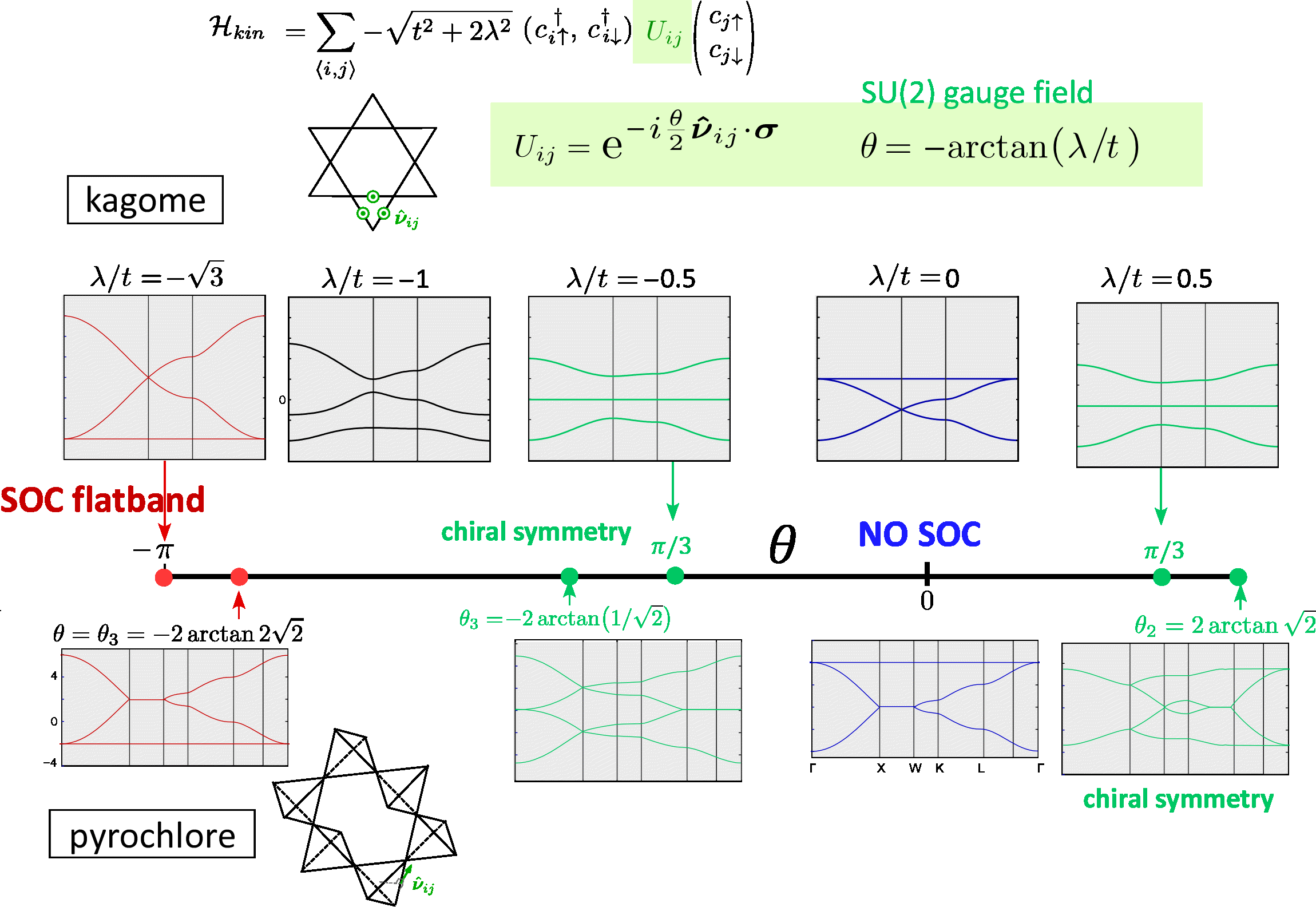
カゴメ格子でH_kinを対角化して得られるバンド構造をθの関数として描いてみると, ２つのflat band, 2つのchiral symmetry が実現します. パイロクロア格子上でも同様です. θ＝０のフラットバンドはよく知られたライングラフ理論のものですがSOC flat bandのほうは我々が新たに 見出したものです. パイロクロアとカゴメの違いは, パイロクロアがθの正負に対して非対称（non abelian SU(2) gauge)なのに対して カゴメは対称(abelian)であることです. これはゲージの可換性・非可換性の違いであり, 格子の形状に対するSOCの入り方で決まります.





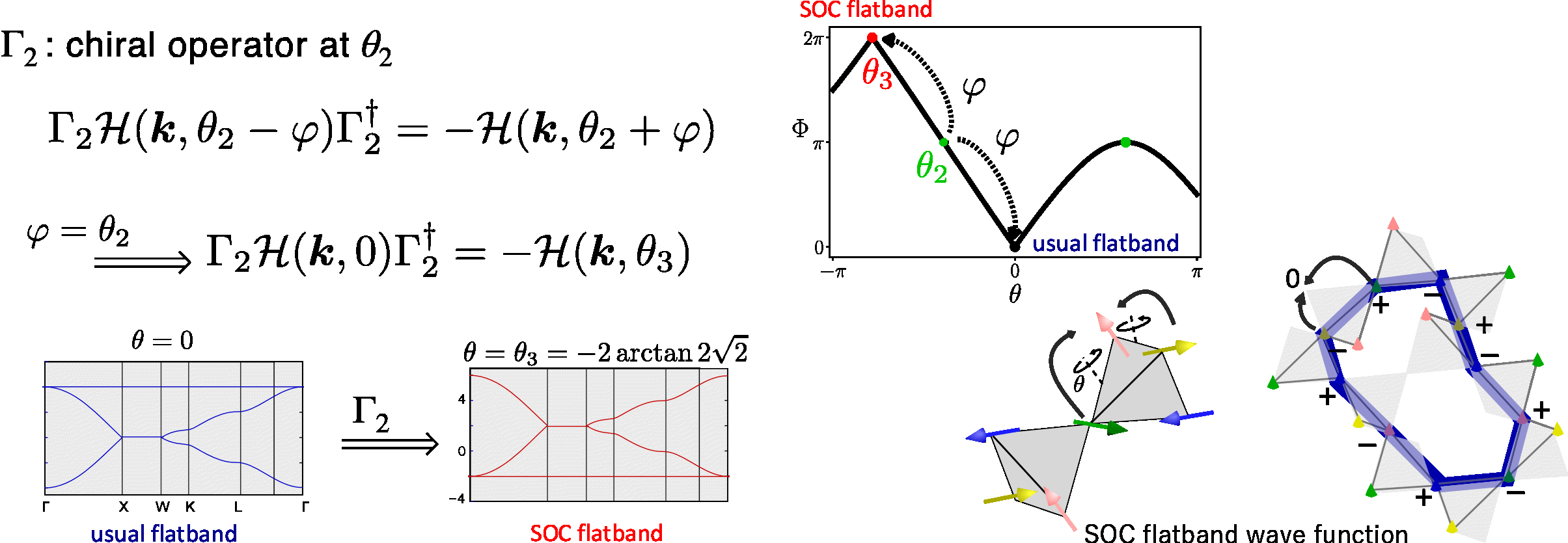
SOC flat band
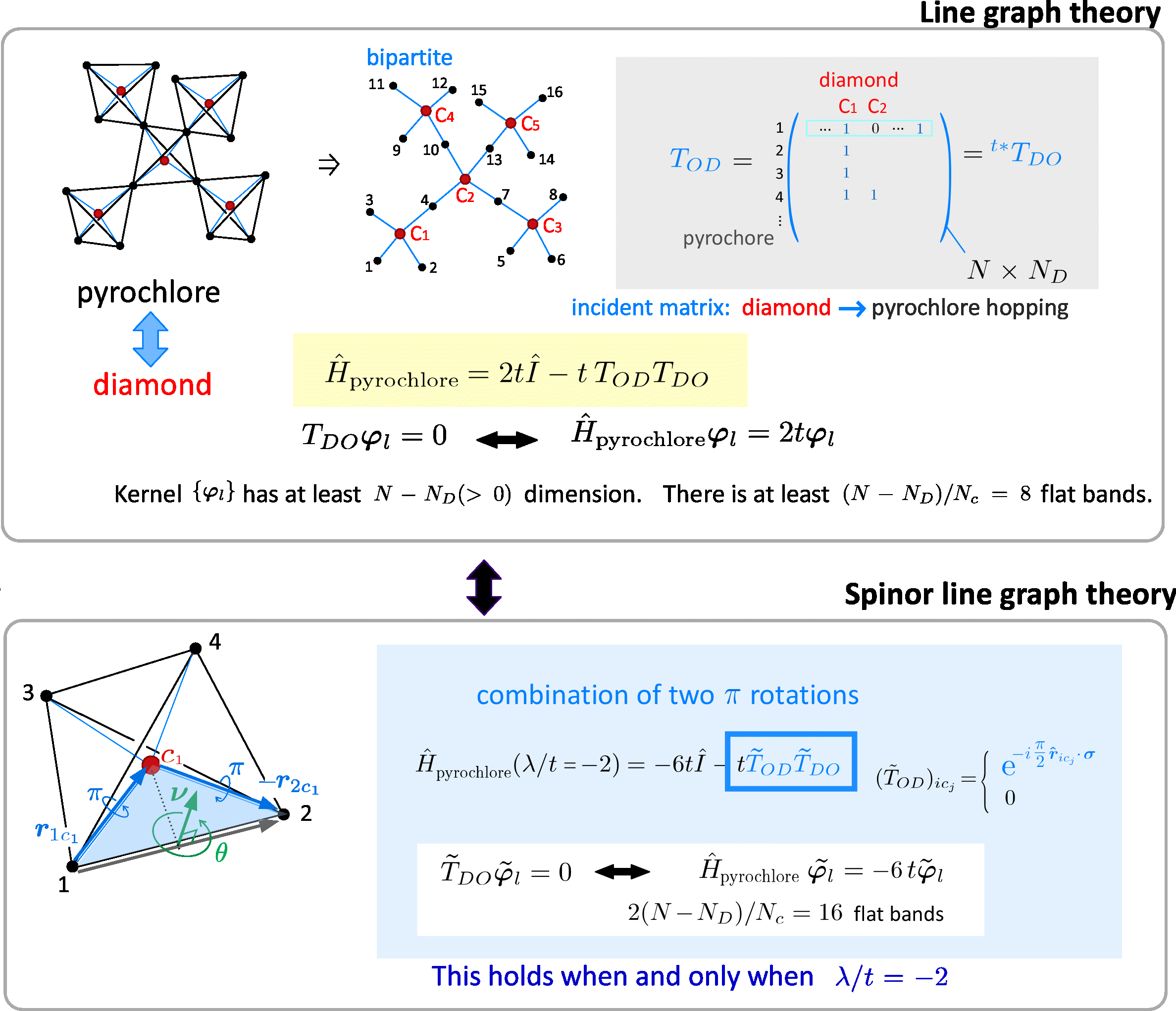
SOCによって電子は飛び移る際にスピンの向きを回転させます. この回転の効果込みで、ライングラフ理論を考えたのが 我々の仕事です. 従来のライングラフ理論をoverviewしてみましょう. まずN個の格子点からなるパイロクロア格子の正四面体の中心に赤丸を置きます, この赤丸同士を結ぶとダイヤモンド格子(N_D個の格子点）が形成されます. ダイヤモンド格子のボンドの中点がちょうどパイロクロアの格子点(黒丸）に相当します. そこでパイロクロア格子のボンドを全部消し, 赤丸と黒丸と青いダイヤモンドの ボンドだけからなるグラフを考えると, これは赤丸と黒丸の二部格子（bipartite=同じ色の格子点は結ばれないグラフ）を構成します. ここで二つの丸の数はそれぞれN_DとNで, 2N_D=Nです. ここで便宜的に incidence matrixという NxN_D行列を用意し, もしi番目のパイロクロア格子点とj番目のダイヤモンド格子点が 青いボンドで結ばれていたらこの行列T_ODのij 成分が１とし, それ以外を０とすると, もとのパイロクロア格子のハミルトニアンH_pyrochloreは T_ODT_DOを使って表せます. というのが, T_DO(=^t*T_OD) でパイロクロアからダイヤモンドへの飛び移りをした電子は, T_ODで パイロクロア格子に再び移るからです. このとき自分自身に戻った分が2tI （対角行列） として余分に生じるのでこれを差っ引いたものが第一項です. もともとT_ODは扁平な行列だったので, T_DOを演算してゼロを返すカーネルの次元は 少なくとも(N-N_D)以上となり, この数だけ H_pyrochloreのりエネルギー固有値が -2tとなるような状態が 生じます. Nはパイロクロアの全格子点の数だったのでバンドの数に焼き直すと, ゆえに(N-N_D)/Nだけflat band が生じるわけです.

SOCがある我々の場合（spinor line graph theory) はスピン自由度分だけ基底が２倍に増えるのですが、それ以外は T_ODが複素数になって回転行列の位相を含むようになっただけで完全に同じ構造を 作り出すことができます. ダイヤモンド格子点を経由して２回飛び移る際ってパイロクロアの隣接サイトに 到達するときにスピンが回転した角度と、回転角θがちょうど 同じになるという条件 のときにflat band が生じます.



Chiral symmetry and local gauge transformation
ここでもう一つの特徴的なバンド構造であるchiral symmetryについて説明してみます. ここでのchiral symmetryはバンド構造の上下対称性であり, グラフェン（ハニカム格子）などでよく 議論された構造です. ハミルトニアンをブロッホ表示したときの表現行列H(k)に関して これと反交換な演算子Γが存在し, このΓでH(k)を変換すると -H(k)となって符号が 反転するとき, Γはchiral演算子と呼ばれます. このときΓを対角化する基底を使うと H(k)の表現が非対角ブロックのみをもつ形となります. ここでは基底が２つのグループに分けられ, 異なったグループ間でしか行列要素が存在しないので、 対角化した後に得られるH(k)の固有状態は自動的に２グループの結合と反結合軌道となり、それらが対称に 上下のペアのバンドを形成します. グラフェンの場合は、黒丸と白丸が等価な２部格子(bipartite)を構成しているので、自明にこのchiral symmetry が存在します. これをBipartite hopping構造とよびます.



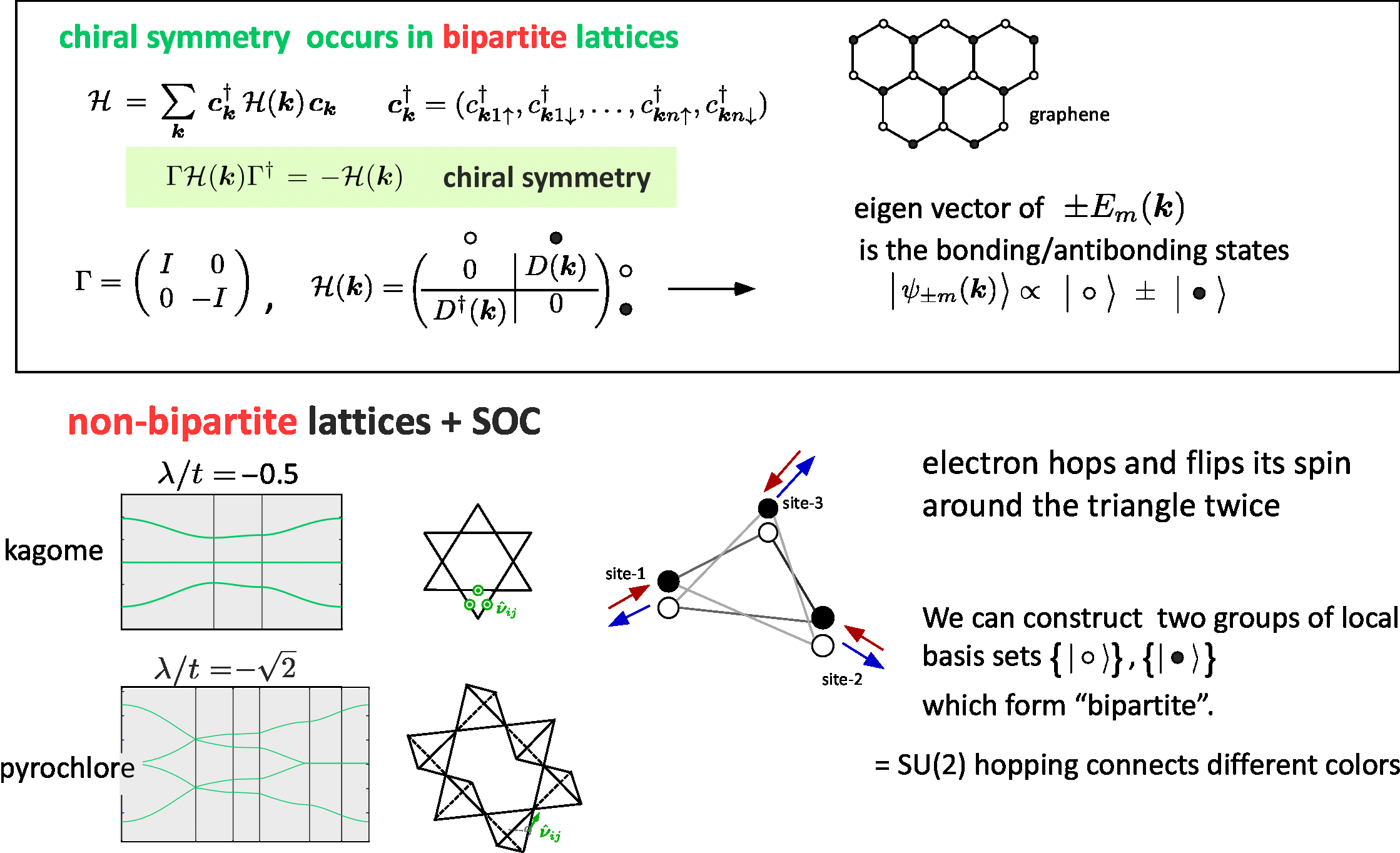
ところが今回のカゴメやパイロクロアの場合は自明な二部格子を形成することが一見困難です. しかしもしスピン自由度を採り入れると, bipartite hopping構造を作り出すことができるということがわかりました. SOCがある場合, 電子は飛び移るときにスピンの向きを回転させます, この向きはθの値できまるうえ, 複雑な格子の上を飛び移ってバンドを形成するので、H(k)は6x6とか8x8のよくわからない表現を持っているので 闇雲に考えてもどのようなことが起きているのかはほぼ絶対にわからないと思います. ここでつかうマジックは、局所ゲージ変換です. 下のほうで詳しく述べますが, 局所ゲージ変換は スピンの量子化軸（ｚの向き）を各サイトごとに好き勝手に変えるような操作であり, この操作のもとで ハミルトニアンの表現は変わりますが固有値は変わりません. ここで都合の良い局所ゲージの取り方をしてやると, 図にあるように三角を形成する site1のある量子化軸に そって上向きだった電子がsite2に飛び移ったとき site2の量子化軸の表現では下向きになり, site3にうつったら 上向きになり, という風に飛び移るたびにスピンの局所的な量子化軸のもとで上下に交互に向きを変えるように してやることができるのです. 三角形を２週回るとスピンの向きは元通りになりますのでこうしてカイラルペアが形成されます. むろんすべてのθでできるわけではなく, うまく局所ゲージを選んでやればこのような操作が可能なθが存在して、それが chiral symmetryの実現する場合になっているのです.

ではこのような局所ゲージ変換は簡単に見つけられるのでしょうか？ いや、そんなに簡単だったらこの話は自明となってしまうのですがそんなわけがなく, ほぼ１００人中99.9人くらいは 予想はできないと思います. そこで Wilson loopという素粒子や物性で古くからよく知られる量を使ってみます.
まず パイロクロアもカゴメもユニットが三角形なので三角形の ループに沿ってSU(2）ゲージ U_ijを３つ掛け合わせたPを定義します. P自体もSU(2）なので一周まわってスピンが角度Φだけ軸n_i,jk周りに 回転したものと見なせます. この量はpath(i;jk)を指定しなくてはならず, 軸n_i,jkはpathに依存しますが Φは依存しない ゲージ不変量です.

このΦのθ依存性を調べると Φ=πのところでchiral symmetryが実現していることがわかります. つまりΦ=πのときには１周回ってスピンが反転しているわけで, １週回るとき奇数のボンドを経るので, １ボンド飛ぶごとに πだけ回転して結果的に トータルでもπ回転しているように, このpath周りの量子化軸を見かけ上取り替えてやることができるのです.
ここでスピン量子化軸とは、一般には全てのサイトで同じz軸を取るのが普通ですが 別に勝手にサイトごとに異なった量子化軸をとってもハミルトニアンの表現が変わるだけで 物理は変わりません. この局所ゲージ変換（スピンの量子化軸の回転）に相当する操作で 結ばれるあらゆる波動関数は基本的に等価で、その選び方にはredundancy (物理的には意味のない任意性)があることは量子力学の基礎的な性質です.



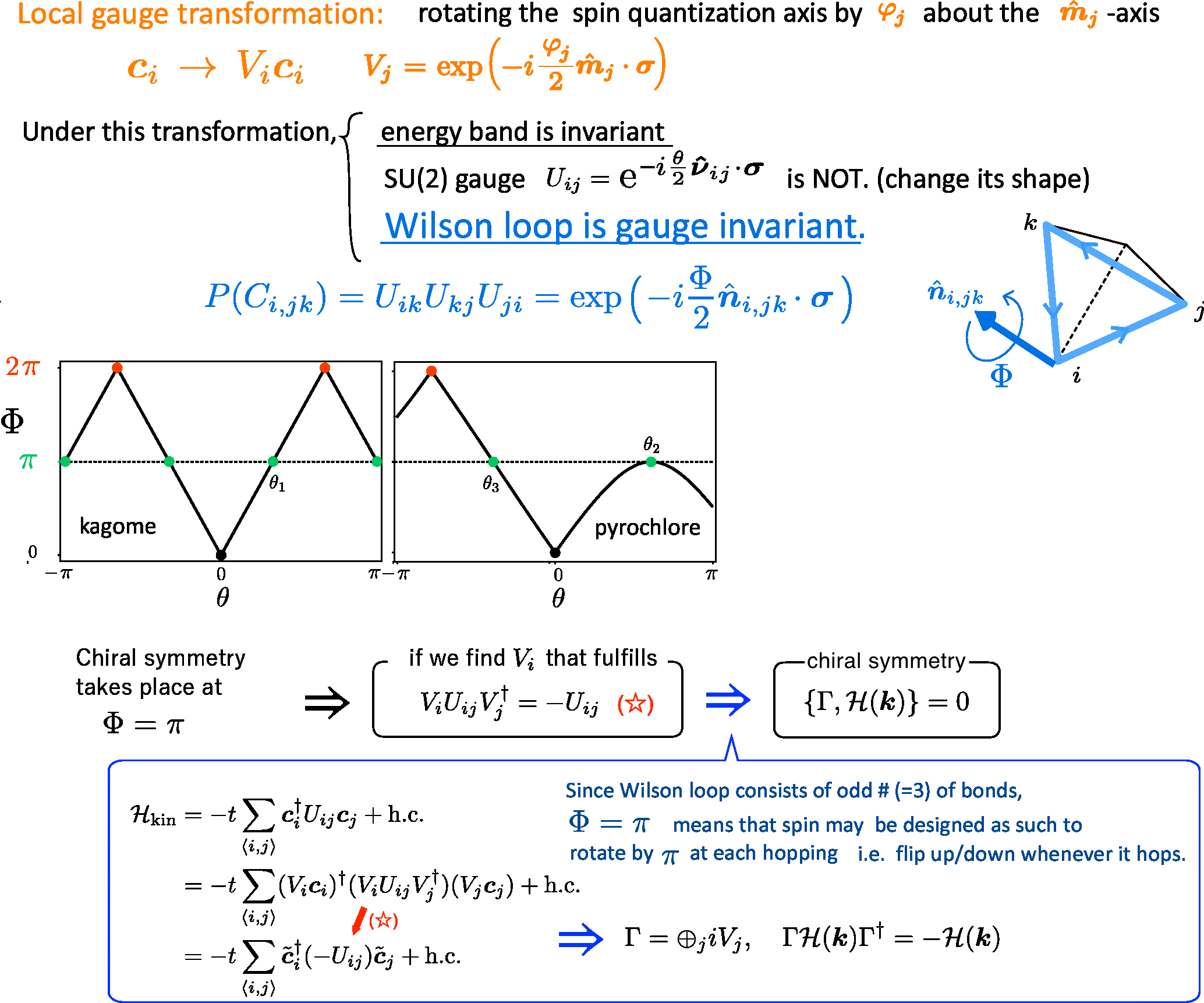
本題に戻り, もし一回飛ぶたびにスピンがπだけ回転するように量子化軸を取り直すような 局所ゲージ変換V_jが存在したならば, この変換によって V_iU_ijV_j⁺= -U_ij のようにSU(2）ゲージ（ホッピングの位相）が符号をかえます. この操作をすべてのボンドijについて行うことによってすべてのU_ijが 符号が反転しハミルトニアン H_kin全体も符号を反転します. ですのでカイラル演算子としては V_jを掛け合わせたものを用意してやれば カイラル対称性が実現するのです. 物理的には, SOCのあるバンド構造で 「スピン量子化軸をうまく局所ゲージ変換で取り直すことによって非自明なカイラルペアを創出した」ことになります.

ここで最後に ... 実はchiral symmetryがあらわれるθ₂で得られる カイラル演算子Γを使って θ＝０のフラットバンドのハミルトニアンを変換すると,バンドが ひっくりかえり、θ(=-π）SOCフラットバンド構造へと変換されるのです. ここで起こっていることは波動関数のレベルではぜんぶ上向きを向いていたスピンが 向きを変えて四面体の４頂点でそれぞれ明後日の方向を向くようになることです. 一見わけのわからないSOC系の構造ですが、その量子力学的性質の深層を解きほぐしてみると 非常に美しい物理的な構造が見えてきます.
ときおり, 実験屋からは 理論的な美しさ以外にフラットバンドって何が面白いの？というセリフがでてくる ことがあるのですが, フラットバンドは究極には、バンドの分散がない強相関極限に相当しています. 実際にホッピングtが有限の値で存在するにもかかわらずなぜ　強相関になるかというと そもそも波動関数が局在して波数ｋが無意味な量となるからです. 局在のメカニズムは, 量子的な干渉効果によって位相がπだけ異なった 電子の伝搬がキャンセルアウトして、たとえば図のようなループの外に電子がでていけなく んってしまうのです. SOCフラットバンドの場合はスピンの回転込々で、 このような干渉効果が起こることが特徴です. このような系は当然, 明らかにアブノーマルでエキゾチックな物性の舞台です. 過去にSOCのもとフラットバンドが実現すればChern数がノンゼロの磁場のない分数量子ホール系が実現するのではないかと いう期待もあったようですがバンドがフラットな場合は, Chern数は絶対にゼロになるということが証明されています. トポロジーは別として, フラットバンドでありながら強磁性でない極限的強相関フラストレート系が実現するのは なかなかレアで今後どうなるかが楽しみな系です.