第21回のウェブ資料
最終更新: 2023/05/23
はじめに(W1)
- 元となるRNA-seqカウントデータ(JSLAB18.csv)
第20回はxlsxファイル(JSLAB18.xlsx)でしたが、今回はcsvファイルを読み込むやり方の紹介を兼ねてJSLAB18.csvを利用します。 - 乳酸菌NGS連載第18回のPDF
- Lactobacillus
rhamnosus GG (LGG)
- Bang et al., J
Microbiol Biotechnol., 2018
- 乳酸菌NGS連載第18回の図5
パラメータの取得(W2)
入力ファイル(JSLAB18.csv)の読込から、群ごとのカウントの平均(\(M\))とdispersion (\(\varPhi\))を得る必要最小限のスクリプトです。
source("https://www.iu.a.u-tokyo.ac.jp/kadota/book/JSLAB21_func.R")
in_f <- "https://www.iu.a.u-tokyo.ac.jp/kadota/book/JSLAB18.csv"
nk <- c(3, 3, 3)
A <- read.csv(in_f, row.names=1, stringsAsFactors=T)
T <- colSums(A)
Anorm <- sweep(x=A, MARGIN=2, STATS=1000000/T, FUN="*")
K <- length(nk)
L <- as.vector(mapply(rep, 1:K, nk))
M <- V <- Phi <- NULL
for(i in 1:K){
M <- cbind(M, apply(X=Anorm[, L==i], MARGIN=1, FUN=mean))
V <- cbind(V, apply(X=Anorm[, L==i], MARGIN=1, FUN=var))
Phi <- cbind(Phi, apply(X=Anorm[, L==i], MARGIN=1, FUN=func_phi))
}NBモデルに従う乱数(W3)
W3.1 \(M\), \(V\), \(\varPhi\)の概要
head関数を用いて、最初の4行分を表示させています。この結果を眺めて、(\(\phi\) > 0と\(\phi \leq\) 0の両方をもつので\(i\) =
2でもよかったのですがなんとなく)\(i\)
=
4に相当するEBG00001128509のパラメータを用いて説明しようと決めました。
head(M, n=4)## [,1] [,2] [,3]
## EBG00001128470 219.35372 139.9754 163.20042
## EBG00001128476 88.02994 116.9911 45.61295
## EBG00001128500 26661.18736 23549.0411 35571.20466
## EBG00001128509 259.62436 166.7145 190.11327head(V, n=4)## [,1] [,2] [,3]
## EBG00001128470 13304.976 246.7638 4.272069e+03
## EBG00001128476 2165.165 178.4106 1.521660e+01
## EBG00001128500 2736641.821 2342808.8423 5.120825e+07
## EBG00001128509 29046.424 151.8007 2.223958e+03head(Phi, n=4)## [,1] [,2] [,3]
## EBG00001128470 0.271959587 0.0054503107 0.15426937
## EBG00001128476 0.268042701 0.0044874537 -0.01460983
## EBG00001128500 0.003812477 0.0041821822 0.04044278
## EBG00001128509 0.427073383 -0.0005365914 0.05627206W3.2 rnbinom関数が正常に動作する場合(\(\varPhi\) > 0)
\(m_{4,3}\) = 190.1133と\(\phi_{4,3}\) = 0.056272をパラメータとして与え、8個の乱数を生成と分散の表示、そして真の値(\(v_{4,3}\) = 2223.958)の表示まで行っています。
i <- 4
k <- 3
M[i,k]## EBG00001128509
## 190.1133Phi[i,k]## EBG00001128509
## 0.05627206set.seed(2023)
output <- rnbinom(n=8, mu=M[i,k], size=1/Phi[i,k])
output## [1] 177 175 153 174 185 206 202 216var(output)## [1] 427.4286V[i,k]## EBG00001128509
## 2223.958次に、同条件で生成させる乱数のみ8個から1000000個に変更して分散を算出し、乱数が増えれば真の値(\(v_{4,3}\) = 2223.958)に近づくことを確認します。
set.seed(2023)
output <- rnbinom(n=1000000, mu=M[i,k], size=1/Phi[i,k])
var(output)## [1] 2224.638W3.3 rnbinom関数のマニュアル
?rnbinomW3.4 ?rnbinom実行直後のスクショ
①のチャンク実行後は、以下に示すような関数マニュアルが②Helpタブ上に見られます。計4つの関数についての説明がなされており、目的の関数は③で見えています。③rnbinomは、n,
size, prob,
muという計4つの引数(Arguments)を受けつけることがわかりますが、それぞれの説明は④に書かれています。
W3.5 rnbinom関数マニュアルのArguments部分
W3.4の続きとして、④Argumentsの⑤sizeに関する説明が見られるようにした状態です。sizeオプションで与える値は、⑥に明記されているように整数(integer)である必要はありませんが、正の値をもたねばなりません。
W3.6 rnbinom関数がエラーとなる場合(\(\phi \leq\) 0)
\(m_{4,2}\) = 166.7145と\(\phi_{4,2}\) = -0.0005365914をパラメータとして与え、8個の乱数を生成と分散の表示まで行っています。
i <- 4
k <- 2
M[i,k]## EBG00001128509
## 166.7145Phi[i,k]## EBG00001128509
## -0.0005365914set.seed(2023)
output <- rnbinom(n=8, mu=M[i,k], size=1/Phi[i,k])## Warning in rnbinom(n = 8, mu = M[i, k], size = 1/Phi[i, k]): NAs producedoutput## [1] NaN NaN NaN NaN NaN NaN NaN NaNvar(output)## [1] NAシミュレーションデータ生成の基本形(W4)
W4.1 第20回の図4
第20回の原稿はモノクロですので、こちらのほうが特に(d)はわかりやすいかと思います。
W4.2 G1群のみの\(\varPhi\) > 0を満たす経験分布を得る
W2のチャンクを実行しておけば、このチャンクをエラーなく実行できます。k <- 1としてG1群に限定し、計2949遺伝子のベクトルに対して、Phi[,k] > 0という条件判定を行い、条件を満たす要素をTRUE、そうでなければFALSEという情報からなるobjを作成しています。sum(obj)は、objがTRUEの要素数を返すので、出力結果が2511というのは妥当です。その後のhead(obj)では、objの最初の6個の要素を出力しています。5番目の要素がFALSEになっていることがわかります。head(Phi[, k])の結果と合わせると、確かに5番目の要素が条件を満たしていないことがわかります。sub_M <- M[obj, k]は、2949行からなるM[, k]の中から、objがTRUEとなる行のみをsub_Mに格納せよというコマンドです。結果として得られるsub_Mは、2511個の要素からなる数値ベクトルになります。sub_Phi <- Phi[obj, k]についても同じノリで、平均の行列Mの部分がdispersionの行列Phiになっているだけです。ここのスクリプトは、わかりやすさ(説明のしやすさ)重視で汎用性は低いのでご注意ください。
k <- 1
obj <- (Phi[,k] > 0)
sum(obj)## [1] 2511head(obj)## EBG00001128470 EBG00001128476 EBG00001128500 EBG00001128509 EBG00001128529
## TRUE TRUE TRUE TRUE FALSE
## LGG_00001
## TRUEhead(Phi[, k])## EBG00001128470 EBG00001128476 EBG00001128500 EBG00001128509 EBG00001128529
## 0.271959587 0.268042701 0.003812477 0.427073383 0.000000000
## LGG_00001
## 0.002775528sub_M <- M[obj, k]
sub_Phi <- Phi[obj, k]W4.3 経験分布の記載例
Kadota et al.,
Algorithms Mol Biol, 2012では、以下のような記載をしています。
To mimic this mean-dispersion relationship in the simulation, we used an
empirical distribution of these values (\(\mu\) and \(\phi\)) calculated from Arabidopsis data
available in the NBPSeq
package.
2012年の論文は、TCCに実装されているDEGES正規化法の原著論文です。TCCで生成しているシミュレーションデータは、モデル植物であるシロイヌナズナのリアルカウントデータから経験分布を得ているということですね。
W4.4 生成予定の遺伝子数分のパラメータ情報を取得
遺伝子数が\(G_{sim}\) =
4の例を示します。s_numは、sample関数を用いて、1:length(sub_M)の整数ベクトルの中から、S_simで指定した個数を、復元抽出(replace=TRUE)した結果であり、計4個の整数の要素からなる数値ベクトルです。sub_M[s_num]は、W4.2で作成したsub_Mの要素の中から、s_numで指定した要素の情報のみを抽出していることに相当します。sub_Phi[s_num]についても同様です。match関数は、この場合はtable=rownames(M))で指定している行列Mの行名情報(つまりrownames(M))の文字列ベクトルの中から、x=names(sub_M[s_num])で指定した文字列ベクトル中の要素と一致するインデックス(要素番号)情報を返します。最終行のc("A", "B", "C", "D", "E")の中からc("D", "B")中の要素と一致するインデックス情報として4と2が返されているのをみると全体像がよくわかると思います。
G_sim <- 4
set.seed(2023)
s_num <- sample(1:length(sub_M), G_sim, replace=TRUE)
s_num## [1] 1909 1488 2479 1385sub_M[s_num]## LGG_02238 LGG_01737 LGG_02907 LGG_01623
## 875.46580 60.89932 274.83665 89.63483sub_Phi[s_num]## LGG_02238 LGG_01737 LGG_02907 LGG_01623
## 0.22292266 0.16477002 0.11164579 0.04881805match(x=names(sub_M[s_num]), table=rownames(M))## [1] 2243 1742 2912 1628match(x=c("D", "B"), table=c("A", "B", "C", "D", "E"))## [1] 4 2W4.5 乱数を生成(べた書き版)
遺伝子数が\(G_{sim}\) =
4、反復数が\(n_{sim}\) =
5の例を示します。s_num[1] = 1909、s_num[2] =
1488、s_num[3] = 2479、s_num[4] =
1385が代入されて、このインデックスに対応する平均とdispersionを入力として乱数がn_sim個分だけ生成されます。ここはあくまでもW4.6が難解であったヒト用です。
n_sim <- 5
set.seed(2023)
i <- 1
rnbinom(n=n_sim, mu=sub_M[s_num[i]], size=1/sub_Phi[s_num[i]])## [1] 738 705 445 643 733i <- 2
rnbinom(n=n_sim, mu=sub_M[s_num[i]], size=1/sub_Phi[s_num[i]])## [1] 67 65 73 92 41i <- 3
rnbinom(n=n_sim, mu=sub_M[s_num[i]], size=1/sub_Phi[s_num[i]])## [1] 219 198 343 171 204i <- 4
rnbinom(n=n_sim, mu=sub_M[s_num[i]], size=1/sub_Phi[s_num[i]])## [1] 106 100 94 108 113W4.6 乱数を生成(forループ版)
遺伝子数が\(G_{sim}\) =
4、反復数が\(n_{sim}\) =
5の例を示します。simdata <- NULLは、ただの”これからsimdataという名前のオブジェクトに具体的な数値情報を入れていくので、まずは場所の確保だけしときますよ(プレースホルダの作成)“という宣言です。for(i in 1:G_sim)は、iという変数を使って、1からG_simまで1づつカウントアップし、{}で囲った範囲のコマンドを実行せよという意味です。hogeの中身は、ただのrnbinom関数実行結果であり、n_sim個の乱数からなる数値ベクトルです。その次の行のrbind関数は、既に存在するsimdataオブジェクトの下の行にhogeを追加せよ、という指令です。たとえば、i
=
1のときは、simdata <- rbind(simdata, hoge)実行結果として得られるsimdataの中身は1行5列の行列となり、その中身はs_num[1]
=
1909で乱数を発生させた結果のhogeと同じです。i
=
2のときは、既に存在する1行5列のsimdataの下の行にs_num[2]
=
1488で乱数を発生させた結果のhogeが追加され2行5列のsimdataになる、といった具合です。
G_sim <- 4
n_sim <- 5
set.seed(2023)
simdata <- NULL
for(i in 1:G_sim){
hoge <- rnbinom(n=n_sim, mu=sub_M[s_num[i]], size=1/sub_Phi[s_num[i]])
simdata <- rbind(simdata, hoge)
}
simdata## [,1] [,2] [,3] [,4] [,5]
## hoge 738 705 445 643 733
## hoge 67 65 73 92 41
## hoge 219 198 343 171 204
## hoge 106 100 94 108 113W4.7 行ごとの分散
まず、行列simdataに対して、行名と列名を付加しています。その後、apply関数を用いて、行ごと(MARGIN=1)に、分散(FUN=var)を計算しています。他には、たとえば列ごとに総和を計算したい場合は、MARGIN=2とFUN=sumとします。posiは、W4.4で得た\(\varPhi\) >
0を満たすG1群の2511個からランダム抽出したs_numから、遺伝子名情報の文字列の一致を頼りに同定した、大元の2949遺伝子の中でのインデックス(要素番号)情報です。最後にそのposiの行かつG1群の列(つまり1列目)の分散情報を表示させています。
rownames(simdata) <- paste("gene", 1:G_sim, sep="")
colnames(simdata) <- paste("rep", 1:n_sim, sep="_")
simdata## rep_1 rep_2 rep_3 rep_4 rep_5
## gene1 738 705 445 643 733
## gene2 67 65 73 92 41
## gene3 219 198 343 171 204
## gene4 106 100 94 108 113apply(X=simdata, MARGIN=1, FUN=var)## gene1 gene2 gene3 gene4
## 14923.2 334.8 4506.5 54.2posi <- match(x=names(sub_M[s_num]), table=rownames(M))
posi## [1] 2243 1742 2912 1628V[posi, 1]## LGG_02238 LGG_01737 LGG_02907 LGG_01623
## 171732.3881 671.9864 8708.0225 481.8588W4.8 反復数を増やして検証
反復数が\(n_{sim}\) = 500000の例です。これくらい反復数を増やすと、正解にかなり近い値が得られることが実感できます。
G_sim <- 4
n_sim <- 500000
set.seed(2023)
simdata <- NULL
for(i in 1:G_sim){
hoge <- rnbinom(n=n_sim, mu=sub_M[s_num[i]], size=1/sub_Phi[s_num[i]])
simdata <- rbind(simdata, hoge)
}
apply(X=simdata, MARGIN=1, FUN=var)## hoge hoge hoge hoge
## 171990.2270 670.3646 8688.4658 482.0801posi <- match(x=names(sub_M[s_num]), table=rownames(M))
V[posi, 1]## LGG_02238 LGG_01737 LGG_02907 LGG_01623
## 171732.3881 671.9864 8708.0225 481.8588W4.9 復元抽出の意味
ここのチャンクは、前半がW4.2、そして後半がW4.4を合わせたものになっています。乱数取得のための元情報length(sub_M)がG_sim未満であれば、sample関数実行時に非復元抽出(replace=FALSE)で行うとエラーが出ることを示しています。
k <- 1
obj <- (Phi[,k] > 0)
sub_M <- M[obj, k]
sub_Phi <- Phi[obj, k]
length(sub_M)## [1] 2511G_sim <- 3000
set.seed(2023)
s_num <- sample(1:length(sub_M), G_sim, replace=FALSE)## Error in sample.int(length(x), size, replace, prob): cannot take a sample larger than the population when 'replace = FALSE'W4.10 遺伝子数10000でシミュレーションデータを生成
G_sim = 10000、n_sim =
5でシミュレーションデータを生成し、行数と列数を確認するところまでです。W2実行後であれば、ここのチャンクが正常に動作するはずです。
k <- 1
G_sim <- 10000
n_sim <- 5
set.seed(2023)
obj <- (Phi[,k] > 0)
sub_M <- M[obj, k]
sub_Phi <- Phi[obj, k]
s_num <- sample(1:length(sub_M), G_sim, replace=TRUE)
simdata <- NULL
for(i in 1:G_sim){
hoge <- rnbinom(n=n_sim, mu=sub_M[s_num[i]], size=1/sub_Phi[s_num[i]])
simdata <- rbind(simdata, hoge)
}
rownames(simdata) <- paste("gene", 1:G_sim, sep="")
colnames(simdata) <- paste("rep", 1:n_sim, sep="_")
dim(simdata)## [1] 10000 5平均-分散プロットの基本形(W5)
第20回のW9.7に対応するプロットの基本形です。
W5.1 G1群のシミュレーションデータ
リアルデータと数を揃えるべく、G_sim =
2949、n_sim =
3でシミュレーションデータを生成し、平均-分散プロットを描画します。2949行×3列のシミュレーションデータのオブジェクトsimdataを作成する基本形はW4.10と同じです。その後は、第20回のW9.7と似たようなノリでプロット作業を行っています。具体的には、simdataの遺伝子(行)ごとの平均M_simと分散V_simを作成し、それらをdata.frame関数を用いて列方向でマージした結果をdオブジェクトに格納しています。そして、第20回のW9.7.2をテンプレートとしてプロットしています。
k <- 1
G_sim <- 2949
n_sim <- 3
set.seed(2023)
obj <- (Phi[,k] > 0)
sub_M <- M[obj, k]
sub_Phi <- Phi[obj, k]
s_num <- sample(1:length(sub_M), G_sim, replace=TRUE)
simdata <- NULL
for(i in 1:G_sim){
hoge <- rnbinom(n=n_sim, mu=sub_M[s_num[i]], size=1/sub_Phi[s_num[i]])
simdata <- rbind(simdata, hoge)
}
rownames(simdata) <- paste("gene", 1:G_sim, sep="")
colnames(simdata) <- paste("rep", 1:n_sim, sep="_")
dim(simdata)## [1] 2949 3simdata_norm <- sweep(x=simdata, MARGIN=2, STATS=1000000/colSums(simdata), FUN="*")
M_sim <- apply(X=simdata_norm, MARGIN=1, FUN=mean)
V_sim <- apply(X=simdata_norm, MARGIN=1, FUN=var)
Phi_sim <- apply(X=simdata_norm, MARGIN=1, FUN=func_phi)
d <- data.frame(MEAN = M_sim,
VARIANCE = V_sim,
DISPERSION = Phi_sim)
library(ggplot2)## Warning: package 'ggplot2' was built under R version 4.1.2coloor <- "magenta"
axis_range <- c(1e-01, 1e+7)
g <- ggplot(d, aes(x=MEAN, y=VARIANCE)) +
geom_point(show.legend = FALSE, alpha=0.45, shape=19, size=0.4, col=coloor) +
scale_x_log10() +
scale_y_log10() +
theme_bw() +
geom_abline(intercept=0, slope=1, color="blue") +
coord_cartesian(xlim=axis_range, ylim=axis_range) +
labs(x="Mean",y="Variance")
plot(g)## Warning: Transformation introduced infinite values in continuous x-axis## Warning: Transformation introduced infinite values in continuous y-axisd1_sim <- d
g1_sim <- gW5.2 G1群のリアルデータ
実質的に第20回のW9.7.2と同じですが、data.frame関数を用いてマージする部分を最初からG1群のみのデータにするなど若干変更しています。今回のW2を実行していれば、MとVのオブジェクトが利用可能なはずですので、ここのチャンクを実行可能です。なお、k <- 1は、G1群のみに限定するという意味で、抽出したい列のインデックス情報に相当します。
k <- 1
d <- data.frame(MEAN = M[, k],
VARIANCE = V[, k])
library(ggplot2)
coloor <- "magenta"
axis_range <- c(1e-01, 1e+7)
g <- ggplot(d, aes(x=MEAN, y=VARIANCE)) +
geom_point(show.legend = FALSE, alpha=0.45, shape=19, size=0.4, col=coloor) +
scale_x_log10() +
scale_y_log10() +
theme_bw() +
geom_abline(intercept=0, slope=1, color="blue") +
coord_cartesian(xlim=axis_range, ylim=axis_range) +
labs(x="Mean",y="Variance")
plot(g)## Warning: Transformation introduced infinite values in continuous x-axis## Warning: Transformation introduced infinite values in continuous y-axisd1_real <- d
g1_real <- gW5.3 G2群のシミュレーションデータ
W5.1と基本的に同じで、G2群について行っています。
k <- 2
G_sim <- 2949
n_sim <- 3
set.seed(2023)
obj <- (Phi[,k] > 0)
sub_M <- M[obj, k]
sub_Phi <- Phi[obj, k]
s_num <- sample(1:length(sub_M), G_sim, replace=TRUE)
simdata <- NULL
for(i in 1:G_sim){
hoge <- rnbinom(n=n_sim, mu=sub_M[s_num[i]], size=1/sub_Phi[s_num[i]])
simdata <- rbind(simdata, hoge)
}
rownames(simdata) <- paste("gene", 1:G_sim, sep="")
colnames(simdata) <- paste("rep", 1:n_sim, sep="_")
dim(simdata)## [1] 2949 3simdata_norm <- sweep(x=simdata, MARGIN=2, STATS=1000000/colSums(simdata), FUN="*")
M_sim <- apply(X=simdata_norm, MARGIN=1, FUN=mean)
V_sim <- apply(X=simdata_norm, MARGIN=1, FUN=var)
Phi_sim <- apply(X=simdata_norm, MARGIN=1, FUN=func_phi)
d <- data.frame(MEAN = M_sim,
VARIANCE = V_sim,
DISPERSION = Phi_sim)
library(ggplot2)
coloor <- "navy"
axis_range <- c(1e-01, 1e+7)
g <- ggplot(d, aes(x=MEAN, y=VARIANCE)) +
geom_point(show.legend = FALSE, alpha=0.45, shape=19, size=0.4, col=coloor) +
scale_x_log10() +
scale_y_log10() +
theme_bw() +
geom_abline(intercept=0, slope=1, color="blue") +
coord_cartesian(xlim=axis_range, ylim=axis_range) +
labs(x="Mean",y="Variance")
plot(g)## Warning: Transformation introduced infinite values in continuous x-axis## Warning: Transformation introduced infinite values in continuous y-axisd2_sim <- d
g2_sim <- gW5.4 G2群のリアルデータ
W5.2と基本的に同じで、G2群について行っています。
k <- 2
d <- data.frame(MEAN = M[, k],
VARIANCE = V[, k])
library(ggplot2)
coloor <- "navy"
axis_range <- c(1e-01, 1e+7)
g <- ggplot(d, aes(x=MEAN, y=VARIANCE)) +
geom_point(show.legend = FALSE, alpha=0.45, shape=19, size=0.4, col=coloor) +
scale_x_log10() +
scale_y_log10() +
theme_bw() +
geom_abline(intercept=0, slope=1, color="blue") +
coord_cartesian(xlim=axis_range, ylim=axis_range) +
labs(x="Mean",y="Variance")
plot(g)## Warning: Transformation introduced infinite values in continuous x-axis## Warning: Transformation introduced infinite values in continuous y-axisd2_real <- d
g2_real <- gW5.5 複数プロットのレイアウト
作成済みの描画用オブジェクトであるg1_real、g1_sim、g2_real、g2_simが4つ存在するという前提で行います。基本的には表示させたい順に記載していくだけです。最後にplot_layout(ncol=2)とやっていますが、これは列数を2つに限定せよという指令です。
library(patchwork)
g1_real + g2_real + g1_sim + g2_sim + plot_layout(ncol=2)平均-分散プロットの発展形(W6)
第20回のW9.8に対応するプロットの発展形です。ggplot関数実行時に、geom_abline(intercept=0.4, slope=1.6, color="gray")として追加された灰色の実線は、計4種類のプロットを眺めて、分散が全体的に小さいG2群のプロットがほぼこの灰色の実線の右下となるようなパラメータ(つまりintercept=0.4とslope=1.6)を目視で定めています。
W6.1 G1群のシミュレーションデータ
W5.1と第20回のW9.8.2をテンプレートとしてプロットしています。
k <- 1
G_sim <- 2949
n_sim <- 3
set.seed(2023)
obj <- (Phi[,k] > 0)
sub_M <- M[obj, k]
sub_Phi <- Phi[obj, k]
s_num <- sample(1:length(sub_M), G_sim, replace=TRUE)
simdata <- NULL
for(i in 1:G_sim){
hoge <- rnbinom(n=n_sim, mu=sub_M[s_num[i]], size=1/sub_Phi[s_num[i]])
simdata <- rbind(simdata, hoge)
}
rownames(simdata) <- paste("gene", 1:G_sim, sep="")
colnames(simdata) <- paste("rep", 1:n_sim, sep="_")
dim(simdata)## [1] 2949 3simdata_norm <- sweep(x=simdata, MARGIN=2, STATS=1000000/colSums(simdata), FUN="*")
M_sim <- apply(X=simdata_norm, MARGIN=1, FUN=mean)
V_sim <- apply(X=simdata_norm, MARGIN=1, FUN=var)
Phi_sim <- apply(X=simdata_norm, MARGIN=1, FUN=func_phi)
d <- data.frame(MEAN = M_sim,
VARIANCE = V_sim,
DISPERSION = Phi_sim)
Vlow <- sum(d[,1] > d[,2])
Vhigh <- sum(d[,1] < d[,2])
library(ggplot2)
coloor <- "magenta"
axis_range <- c(1e-01, 1e+7)
g <- ggplot(d, aes(x=MEAN, y=VARIANCE)) +
geom_point(show.legend = FALSE, alpha=0.45, shape=19, size=0.4, col=coloor) +
scale_x_log10() +
scale_y_log10() +
theme_bw() +
geom_abline(intercept=0, slope=1, color="blue") +
geom_abline(intercept=0.4, slope=1.6, color="gray") +
coord_cartesian(xlim=axis_range, ylim=axis_range) +
labs(x="Mean",y="Variance") +
annotate("text", x=1e+06, y=1e+00, label=Vlow) +
annotate("text", x=1e+00, y=1e+06, label=Vhigh)
plot(g)## Warning: Transformation introduced infinite values in continuous x-axis## Warning: Transformation introduced infinite values in continuous y-axisd1_sim <- d
g1_sim <- gW6.2 G1群のリアルデータ
W5.2と第20回のW9.8.2をテンプレートとしてプロットしています。
k <- 1
d <- data.frame(MEAN = M[, k],
VARIANCE = V[, k],
DISPERSION = Phi[, k])
Vlow <- sum(d[,1] > d[,2])
Vhigh <- sum(d[,1] < d[,2])
library(ggplot2)
coloor <- "magenta"
axis_range <- c(1e-01, 1e+7)
g <- ggplot(d, aes(x=MEAN, y=VARIANCE)) +
geom_point(show.legend = FALSE, alpha=0.45, shape=19, size=0.4, col=coloor) +
scale_x_log10() +
scale_y_log10() +
theme_bw() +
geom_abline(intercept=0, slope=1, color="blue") +
geom_abline(intercept=0.4, slope=1.6, color="gray") +
coord_cartesian(xlim=axis_range, ylim=axis_range) +
labs(x="Mean",y="Variance") +
annotate("text", x=1e+06, y=1e+00, label=Vlow) +
annotate("text", x=1e+00, y=1e+06, label=Vhigh)
plot(g)## Warning: Transformation introduced infinite values in continuous x-axis## Warning: Transformation introduced infinite values in continuous y-axisd1_real <- d
g1_real <- gW6.3 G2群のシミュレーションデータ
W5.3と第20回のW9.8.2をテンプレートとしてプロットしています。
k <- 2
G_sim <- 2949
n_sim <- 3
set.seed(2023)
obj <- (Phi[,k] > 0)
sub_M <- M[obj, k]
sub_Phi <- Phi[obj, k]
s_num <- sample(1:length(sub_M), G_sim, replace=TRUE)
simdata <- NULL
for(i in 1:G_sim){
hoge <- rnbinom(n=n_sim, mu=sub_M[s_num[i]], size=1/sub_Phi[s_num[i]])
simdata <- rbind(simdata, hoge)
}
rownames(simdata) <- paste("gene", 1:G_sim, sep="")
colnames(simdata) <- paste("rep", 1:n_sim, sep="_")
dim(simdata)## [1] 2949 3simdata_norm <- sweep(x=simdata, MARGIN=2, STATS=1000000/colSums(simdata), FUN="*")
M_sim <- apply(X=simdata_norm, MARGIN=1, FUN=mean)
V_sim <- apply(X=simdata_norm, MARGIN=1, FUN=var)
Phi_sim <- apply(X=simdata_norm, MARGIN=1, FUN=func_phi)
d <- data.frame(MEAN = M_sim,
VARIANCE = V_sim,
DISPERSION = Phi_sim)
Vlow <- sum(d[,1] > d[,2])
Vhigh <- sum(d[,1] < d[,2])
library(ggplot2)
coloor <- "navy"
axis_range <- c(1e-01, 1e+7)
g <- ggplot(d, aes(x=MEAN, y=VARIANCE)) +
geom_point(show.legend = FALSE, alpha=0.45, shape=19, size=0.4, col=coloor) +
scale_x_log10() +
scale_y_log10() +
theme_bw() +
geom_abline(intercept=0, slope=1, color="blue") +
geom_abline(intercept=0.4, slope=1.6, color="gray") +
coord_cartesian(xlim=axis_range, ylim=axis_range) +
labs(x="Mean",y="Variance") +
annotate("text", x=1e+06, y=1e+00, label=Vlow) +
annotate("text", x=1e+00, y=1e+06, label=Vhigh)
plot(g)## Warning: Transformation introduced infinite values in continuous x-axis## Warning: Transformation introduced infinite values in continuous y-axisd2_sim <- d
g2_sim <- gW6.4 G2群のリアルデータ
W5.4と第20回のW9.8.2をテンプレートにしています。
k <- 2
d <- data.frame(MEAN = M[, k],
VARIANCE = V[, k],
DISPERSION = Phi[, k])
Vlow <- sum(d[,1] > d[,2])
Vhigh <- sum(d[,1] < d[,2])
library(ggplot2)
coloor <- "navy"
axis_range <- c(1e-01, 1e+7)
g <- ggplot(d, aes(x=MEAN, y=VARIANCE)) +
geom_point(show.legend = FALSE, alpha=0.45, shape=19, size=0.4, col=coloor) +
scale_x_log10() +
scale_y_log10() +
theme_bw() +
geom_abline(intercept=0, slope=1, color="blue") +
geom_abline(intercept=0.4, slope=1.6, color="gray") +
coord_cartesian(xlim=axis_range, ylim=axis_range) +
labs(x="Mean",y="Variance") +
annotate("text", x=1e+06, y=1e+00, label=Vlow) +
annotate("text", x=1e+00, y=1e+06, label=Vhigh)
plot(g)## Warning: Transformation introduced infinite values in continuous x-axis## Warning: Transformation introduced infinite values in continuous y-axisd2_real <- d
g2_real <- gW6.5 複数プロットのレイアウトの基本形
第20回のW9.7.3をテンプレートにしています。作成済みの描画用オブジェクトであるg1_real、g1_sim、g2_real、g2_simが4つ存在するという前提で行います。基本的には表示させたい順に記載していくだけです。最後にplot_layout(ncol=2)とやっていますが、これは列数を2つに限定せよという指令です。
g1_real + g2_real + g1_sim + g2_sim + plot_layout(ncol=2)W6.6 複数プロットのレイアウトの本番
第20回のW9.8.3をテンプレートにしています。これが図4の原形です。
g <- g1_real + g2_real + g1_sim + g2_sim + plot_layout(ncol=2)
ggsave("JSLAB21.w6.6.png", g, units="px", width=1900, height=1760, device="png")得られたJSLAB21.w6.6.pngは、以下に見えているものと同じになります。
W6.7 dispersionパラメータ\(\varPhi\)の値の分布
\(\varPhi\) >
0という条件を満たす\(\varPhi\)の分布をG1群(k <- 1)とG2群(k <- 2)それぞれについて示しています。
k <- 1
obj <- (Phi[,k] > 0)
summary(Phi[obj, k])## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000065 0.0336613 0.1024031 0.2001206 0.2647383 2.8600830k <- 2
obj <- (Phi[,k] > 0)
summary(Phi[obj, k])## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000001 0.0030773 0.0076807 0.0231526 0.0186456 1.6794190G1群のリアルデータの情報はd1_realに、G2群のリアルデータの情報はd2_realに、G1群のシミュレーションデータの情報はd1_simに、G2群のシミュレーションデータの情報はd2_simに、それぞれ格納しているので、以下のような書き方でもかまいません。一旦hogeというオブジェクトにコピーして使用することで、その下のobjを得るコマンドやsummary関数部分のコマンドを同じにして使いまわせるという利点があります。
hoge <- d1_real
obj <- (hoge$DISPERSION > 0)
summary(hoge$DISPERSION[obj])## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000065 0.0336613 0.1024031 0.2001206 0.2647383 2.8600830hoge <- d2_real
obj <- (hoge$DISPERSION > 0)
summary(hoge$DISPERSION[obj])## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000001 0.0030773 0.0076807 0.0231526 0.0186456 1.6794190hoge <- d1_sim
obj <- (hoge$DISPERSION > 0)
summary(hoge$DISPERSION[obj])## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000461 0.0245210 0.0804688 0.1967201 0.2437880 2.8322877hoge <- d2_sim
obj <- (hoge$DISPERSION > 0)
summary(hoge$DISPERSION[obj])## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000064 0.0031789 0.0108589 0.0388873 0.0317629 1.6623120シミュレーションデータ生成の発展形(W7)
W7.1 \(\varPhi\) > 0を満たす経験分布を得る
W4.2の発展形として、計3群全ての平均\(M\)とdispersion\(\varPhi\)の情報をシミュレーションデータ作成時の経験分布として利用します。理解のしやすさを重視して、W4.2とR4.6を組み合わせたようなスクリプトにしています。W2のチャンクを実行しておけば、このチャンクをエラーなく実行できます。\(K\)は群数です。appendは、既存のベクトルの末尾に要素を追加する関数であり、cという関数と基本的に同じ機能です。rbindが既存の行列の行末に新たな行を追加する機能をもっていたことを思い出せば、そのベクトル版だと納得できると思います。forで、k番目の群ごとに、最大Kまでループを回し、dispersion情報を格納した行列Phiのk番目の列について、値が0より大きい行をTRUE、それ以外をFALSEとした論理値ベクトルobjを得たのち、その情報を用いてフィルタリングをしています。最終的に得られるsub_Mとsub_Phiの要素数は6026であり、W4.1または第20回の図4(d)で見えている数値と一致していることがわかります。
K <- 3
set.seed(2023)
sub_M <- sub_Phi <- NULL
for(k in 1:K){
obj <- (Phi[,k] > 0)
sub_M <- append(sub_M, M[obj, k])
sub_Phi <- append(sub_Phi, Phi[obj, k])
}
length(sub_M)## [1] 6026length(sub_Phi)## [1] 6026W7.2 全てがnonDEGの数値行列を生成
W4.10をテンプレートとしています。遺伝子数G_simと群ごとの反復数nkを入力として与えて、数値行列simdataを出力として得ています。最終行で、念のためwrite.csv関数を用いて作成したシミュレーションデータをJSLAB21_w7.2.csvという名前で保存しています。
G_sim <- 10000
nk <- c(3, 3)
n_sim <- sum(nk)
set.seed(2023)
s_num <- simdata <- NULL
for(i in 1:G_sim){
hoge1 <- sample(1:length(sub_M), 1, replace=TRUE)
hoge2 <- rnbinom(n=n_sim, mu=sub_M[hoge1], size=1/sub_Phi[hoge1])
s_num <- append(s_num, hoge1)
simdata <- rbind(simdata, hoge2)
}
rownames(simdata) <- paste("gene", 1:G_sim, sep="")
colnames(simdata) <- c(paste("G1_rep", 1:nk[1], sep=""), paste("G2_rep", 1:nk[2], sep=""))
dim(simdata)## [1] 10000 6head(simdata)## G1_rep1 G1_rep2 G1_rep3 G2_rep1 G2_rep2 G2_rep3
## gene1 90 136 99 117 126 144
## gene2 47 50 34 39 34 51
## gene3 791 514 577 663 777 724
## gene4 10 5 9 15 23 9
## gene5 49 64 58 17 30 31
## gene6 257 263 278 278 242 268write.csv(x=simdata, file="JSLAB21_w7.2.csv")W7.3 log2(G2/G1)の算出
W7.2で作成したsimdataオブジェクトがあるという前提で記載しています。群ごとの反復数の情報nkを入力として与えてクラスラベル情報Lを作成し、それに基づいて群ごとのカウントの平均をM_G1およびM_G2として得ています。その後、底が2のlog比をlog2(M_G2/M_G1)として算出した結果をlogratioというオブジェクトに格納しています。summary(logratio)実行結果には-Inf、NaN、そしてInfが表示されていますが、これらはそれぞれG1群が0、両群とも0、そしてG2群が0の場合に相当します。それゆえ、logratioのベクトルに対して、有限かどうかをis.finite関数で判定し、有限である(InfやNaNやNAではない)要素のみでsummary関数を実行しなおしているのがsummary(logratio[obj])になります。logratio[!obj]は、有限ではない(InfやNaNやNAである)要素を表示していることになります。!objとすることでTRUE
or
FALSEが入れ替わることを利用しています。こんな感じで実際のところどの遺伝子が悪さをしているのかを知ることができます。length(logratio[!obj])は、有限ではない(InfやNaNやNAである)要素を表示していることになります。
nk <- c(3, 3)
K <- length(nk)
L <- as.vector(mapply(rep, 1:K, nk))
hoge <- simdata
M_G1 <- apply(X=hoge[, L==1], MARGIN=1, FUN=mean)
M_G2 <- apply(X=hoge[, L==2], MARGIN=1, FUN=mean)
logratio <- log2(M_G2/M_G1)
summary(logratio)## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## -Inf -0.1834 0.0000 NaN 0.1886 Inf 7obj <- is.finite(logratio)
summary(logratio[obj])## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -5.028408 -0.182816 0.000000 -0.000143 0.188445 6.203428logratio[!obj]## gene157 gene391 gene421 gene1183 gene1414 gene2183 gene2369 gene2489
## Inf NaN -Inf Inf NaN -Inf -Inf Inf
## gene2691 gene2946 gene3154 gene3231 gene3638 gene5286 gene5352 gene5850
## Inf Inf Inf -Inf -Inf Inf -Inf Inf
## gene6231 gene6764 gene7028 gene7848 gene8007 gene8313 gene8518 gene8746
## -Inf NaN -Inf NaN NaN -Inf -Inf NaN
## gene8991 gene9177 gene9460 gene9477
## NaN Inf -Inf -Inflength(logratio[!obj])## [1] 28W7.4 ヒストグラム(DEGなし)
W7.3で作成した、log2(M_G2/M_G1)の計算結果に相当するlogratioオブジェクトが存在するという前提で記載しています。最初に、わざわざdata.frame形式にしているのは、ggplot2でのを意識しているためり、log2(M_G2/M_G1)の計算の実体であるlogratioオブジェクトの中身をlog2ratioという列名で取り扱えるようにして、dというオブジェクトに格納しています。そうしているからこそ、ggplot関数の部分で、aes(x=log2ratio)のように書いて指定できるのです。このあたりのノリは、第20回のW8と同じです。
d <- data.frame(log2ratio = logratio)
library(ggplot2)
g <- ggplot(d, aes(x=log2ratio)) +
geom_histogram()
plot(g)
プロットの横軸のラベルが原点の0よりも右側にずれている印象を受けたかもしれませんが、これはsummary(logratio[obj])実行結果を見返していただければ納得できると思います。つまり、有限である(InfやNaNやNAではない)要素のみでsummary関数を実行した結果の最小値が-5.028408、そして最大値が6.203428だからです。たとえば、以下のように、軸の取りうる範囲をc(-4, 4)として与えれば、プロットの横軸のラベルがピタリと原点の0付近に位置するようになります。
d <- data.frame(log2ratio = logratio)
library(ggplot2)
axis_range <- c(-4, 4)
g <- ggplot(d, aes(x=log2ratio)) +
geom_histogram() +
coord_cartesian(xlim=axis_range)
plot(g)
発現変動が2倍L未満に収まっている遺伝子数を調べています。2倍未満というのは、G2群がG1群に比べて1/2倍より大きく2倍より小さい範囲ということを意味します。これは、log2スケールでは、log2(1/2)より大きくlog2(2/1)より小さい範囲ということになり、結局-1より大きく+1より小さい範囲内にある遺伝子数をカウントすればよいということになります。つまり、以下のような条件判定でよいことになります。
obj <- ((logratio[obj] > -1) & (logratio[obj] < 1))
sum(obj)## [1] 9288W7.5 DEGの導入
W7.2で作成したsimdataオブジェクトがあるという前提で記載しています。群ごとの反復数の情報nkを入力として与えてクラスラベル情報Lを作成し、それに基づいてどの群をFC倍するかを与えています。ここでは、simdataと同じ行数と列数の、どの要素を何倍するかという情報からなるfc_matを作成したのち、simdataとfc_matの行列同士を掛けることで目的を達成しています。ここではPDEG
> 0かつP1 <
1.0であるという前提でシンプルに記載しています。なお、(G_sim*PDEG*P1)
= 2250、(G_sim*PDEG*P1+1) = 2251、(G_sim*PDEG)
=
2500です。head(simdata)とhead(simdata_DEG)の比較からも、ちゃんとうまく目的の箇所をFC倍できていることがわかります。fc_mat[((G_sim*PDEG*P1-2):(G_sim*PDEG*P1+3)), ]は、DEG_G1パターンとDEG_G2パターンの切り替わり部分が意図通りに作成できているかを確認しているだけです。最終行で、念のためwrite.csv関数を用いて作成したシミュレーションデータをJSLAB21_w7.5.csvという名前で保存しています。
G_sim <- 10000
nk <- c(3, 3)
PDEG <- 0.25
P1 <- 0.9
FC <- 4
K <- length(nk)
L <- as.vector(mapply(rep, 1:K, nk))
head(simdata)## G1_rep1 G1_rep2 G1_rep3 G2_rep1 G2_rep2 G2_rep3
## gene1 90 136 99 117 126 144
## gene2 47 50 34 39 34 51
## gene3 791 514 577 663 777 724
## gene4 10 5 9 15 23 9
## gene5 49 64 58 17 30 31
## gene6 257 263 278 278 242 268fc_mat <- matrix(1, nrow=G_sim, ncol=sum(nk))
fc_mat[1:(G_sim*PDEG*P1), L==1] <- FC
fc_mat[((G_sim*PDEG*P1+1):(G_sim*PDEG)), L==2] <- FC
fc_mat[((G_sim*PDEG*P1-2):(G_sim*PDEG*P1+3)), ]## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 4 4 4 1 1 1
## [2,] 4 4 4 1 1 1
## [3,] 4 4 4 1 1 1
## [4,] 1 1 1 4 4 4
## [5,] 1 1 1 4 4 4
## [6,] 1 1 1 4 4 4simdata_DEG <- simdata*fc_mat
head(simdata_DEG)## G1_rep1 G1_rep2 G1_rep3 G2_rep1 G2_rep2 G2_rep3
## gene1 360 544 396 117 126 144
## gene2 188 200 136 39 34 51
## gene3 3164 2056 2308 663 777 724
## gene4 40 20 36 15 23 9
## gene5 196 256 232 17 30 31
## gene6 1028 1052 1112 278 242 268write.csv(x=simdata_DEG, file="JSLAB21_w7.5.csv")W7.6 ヒストグラム1(DEGあり)
W7.5で作成したsimdata_DEGとラベル情報Lが存在するという前提です。プロットの-2付近のやや大きめのピークがG1群で高発現のDEG_G1由来のもの、そして+2付近の小さめのピークがG2群で高発現のDEG_G2由来のものです。最後の2行は、作成したシミュレーションデータの右側にobjとlogratioを追加したものJSLAB21_w7.6.csvという名前で保存しています。
hoge <- simdata_DEG
M_G1 <- apply(X=hoge[, L==1], MARGIN=1, FUN=mean)
M_G2 <- apply(X=hoge[, L==2], MARGIN=1, FUN=mean)
logratio <- log2(M_G2/M_G1)
summary(logratio)## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## -Inf -0.9303 -0.0813 NaN 0.1362 Inf 7obj <- is.finite(logratio)
summary(logratio[obj])## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -6.08746 -0.91718 -0.08128 -0.40046 0.13579 6.20343logratio[!obj]## gene157 gene391 gene421 gene1183 gene1414 gene2183 gene2369 gene2489
## Inf NaN -Inf Inf NaN -Inf -Inf Inf
## gene2691 gene2946 gene3154 gene3231 gene3638 gene5286 gene5352 gene5850
## Inf Inf Inf -Inf -Inf Inf -Inf Inf
## gene6231 gene6764 gene7028 gene7848 gene8007 gene8313 gene8518 gene8746
## -Inf NaN -Inf NaN NaN -Inf -Inf NaN
## gene8991 gene9177 gene9460 gene9477
## NaN Inf -Inf -Inflength(logratio[!obj])## [1] 28d <- data.frame(log2ratio = logratio)
library(ggplot2)
axis_range <- c(-4, 4)
g <- ggplot(d, aes(x=log2ratio)) +
geom_histogram() +
coord_cartesian(xlim=axis_range)
plot(g)tmp <- cbind(simdata_DEG, obj, logratio)
write.csv(x=tmp, file="JSLAB21_w7.6.csv")W7.7 ヒストグラム2(DEGあり)
W7.6と基本的に同じですが、1~2250行目のG1群で高発現のDEG_G1、2251~2500行目のG2群で高発現のDEG_G2、そして残りのnonDEGパターンの3種類に分けてプロットするやり方です。facet_gridは、第20回のW9.2.3でも利用しています。
G_sim <- 10000
PDEG <- 0.25
P1 <- 0.9
exp_pat <- rep("nonDEG", G_sim)
exp_pat[1:(G_sim*PDEG*P1)] <- "DEG_G1"
exp_pat[(G_sim*PDEG*P1+1):(G_sim*PDEG)] <- "DEG_G2"
d <- data.frame(log2ratio = logratio,
Pattern = exp_pat)
library(ggplot2)
axis_range <- c(-4, 4)
g <- ggplot(d, aes(x=log2ratio, color=Pattern)) +
geom_histogram() +
coord_cartesian(xlim=axis_range) +
facet_grid(rows=vars(Pattern))
plot(g)
ちなみに、上のスクリプトはggplot(d, aes(x=log2ratio, color=Pattern))としましたが、これを以下で示すようにggplot(d, aes(x=log2ratio, fill=Pattern))のようにすると、外枠だけでなく中も塗りつぶすことができます。
G_sim <- 10000
PDEG <- 0.25
P1 <- 0.9
exp_pat <- rep("nonDEG", G_sim)
exp_pat[1:(G_sim*PDEG*P1)] <- "DEG_G1"
exp_pat[(G_sim*PDEG*P1+1):(G_sim*PDEG)] <- "DEG_G2"
d <- data.frame(log2ratio = logratio,
Pattern = exp_pat)
library(ggplot2)
axis_range <- c(-4, 4)
g <- ggplot(d, aes(x=log2ratio, fill=Pattern)) +
geom_histogram() +
coord_cartesian(xlim=axis_range) +
facet_grid(rows=vars(Pattern))
plot(g)W7.8 パターンごとのlog2(G2/G1)分布
“DEG_G1”, “DEG_G2”,
“nonDEG”の3パターンを分けてlog比の分布をsummary関数で得ます。summary(logratio[obj])までは、W7.3をテンプレートとして作成し、全遺伝子の結果を示しています。残りは、W7.7で作成した”どの行番号に相当する要素がどのパターンに属するかを定めたexp_pat“を利用して、特定のパターンに限定してsummary関数を実行しています。”DEG_G1”のMEANが-2.0、“DEG_G2”のMEANが2.0、そして”nonDEG”のMEANが0.0と酷似した値になっており妥当だと判断できます。
hoge <- simdata_DEG
M_G1 <- apply(X=hoge[, L==1], MARGIN=1, FUN=mean)
M_G2 <- apply(X=hoge[, L==2], MARGIN=1, FUN=mean)
logratio <- log2(M_G2/M_G1)
obj <- is.finite(logratio)
summary(logratio[obj])## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -6.08746 -0.91718 -0.08128 -0.40046 0.13579 6.20343summary(logratio[(exp_pat == "DEG_G1") & obj])## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -6.087 -2.170 -2.000 -1.998 -1.809 1.459summary(logratio[(exp_pat == "DEG_G2") & obj])## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -1.807 1.850 1.998 1.998 2.202 3.493summary(logratio[(exp_pat == "nonDEG") & obj])## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -5.028408 -0.188363 0.000000 -0.000647 0.185955 6.203428W7.9 検証
ここでは、一見変な結果のものを見つけ出して確認しています。まず、“DEG_G1”のlog比中で最大値(ただし実数のみ)を示す遺伝子が”gene769”であることを見出し、そのカウント情報を表示する作業を行っています。そして目視で各群のカウントの総和を算出し(本当は平均ですが、数学的には等価です)、手計算でlog比の結果を得て、summary(logratio[(exp_pat == "DEG_G1") & obj])の結果と同じ値になっているところまでを確認して安心しています。次に、“DEG_G2”のlog比中で最小値(ただし実数のみ)を示す遺伝子が”gene2498”であり、そのカウント情報を表示、そしてlog比の検証を行っています。話がややこしくなるので気になったヒトのみでよいですが、which.max(logratio[(exp_pat == "DEG_G1") & obj])の主な結果である766と”gene769”の間に数値上の不一致があると思われたのではないでしょうか。そしてその疑念は、which.min(logratio[(exp_pat == "DEG_G2") & obj])の主な結果である246と”gene2498”の大きな不一致によって確信に変わったと思います。これは、例えばwhich.maxは最大値をとるインデックス情報が返されるのですが、入力の段階でlogratio[(exp_pat
==
“DEG_G1”)に限定されていて、かつlog比が実数のもの(objがTRUEの要素のみ)に限定された状態でのインデックス番号なのだと理解すれば納得できると思います。つまり、exp_pat
==
“DEG_G2”)を入力として与えた段階ですでに入力要素数は250個に限定されています。そしてさらにlog比が実数のもの(objがTRUEの要素のみ)に限定されているので、遺伝子名が”gene2498”だったとしても、出力結果は246番目の要素だという風になるのです。
which.max(logratio[(exp_pat == "DEG_G1") & obj])## gene769
## 766simdata_DEG["gene769",]## G1_rep1 G1_rep2 G1_rep3 G2_rep1 G2_rep2 G2_rep3
## 0 4 0 0 5 6log2(11/4)## [1] 1.459432which.min(logratio[(exp_pat == "DEG_G2") & obj])## gene2498
## 246simdata_DEG["gene2498",]## G1_rep1 G1_rep2 G1_rep3 G2_rep1 G2_rep2 G2_rep3
## 0 12 2 0 0 4log2(4/14)## [1] -1.807355tidyverseの概要(W8)
tidyverseによるパラメータの取得 (W9)
W9.1 パッケージの読み込み
tidyverseは複数のパッケージのコレクションであり、library(tidyverse)の一発で構成するパッケージの提供するすべての関数を利用できるようになります。
library(tidyverse)W9.2 csvファイルの読み込み
tidyverseではデータの読み込みや処理に際して、基本的にtibbleと呼ばれる形式を使います。一般的にRでデータを扱う際にはdata.frame形式が使われますが、tibbleはその拡張版と考えて問題ありません。さらにtidyverseの関数はdata.frame型もサポートしているため、tidyverseによる解析において必ずしもtibble形式を使わなければならない訳ではありません(data.frame形式のデータを可視化する際にggplot2を使用する場合が多いですが、ggplot2はもともとtidyverseのパッケージの1つです)。
このtibbleは”tidy
data”というデータ構造の考え方に基づいて設計されています。tidy
dataは解析を始めるにあたり最適な、“整然とした”データのあり方を定義しており、乱雑なデータから最終的にtidy
dataへと変換することがtidyverseにおける前処理の目的と言えます。tidy
dataの詳細についてはtibbleのリファレンスを参照してください。なお、tidy
dataの定義からしてtibbleでは基本的に行名を持つことはできませんが、どうしても行名を指定したい場合column_to_rownames関数を使って”ふつうの列”から”行名を表す列”に変換する必要があります。一方、列名は最初の1行目が自動的に指定されます。
library(tidyverse)
source_url <- "https://www.iu.a.u-tokyo.ac.jp/kadota/book/JSLAB21_func.R"
input_file_url <- "https://www.iu.a.u-tokyo.ac.jp/kadota/book/JSLAB18.csv"
source(source_url)
A <- read_csv(input_file_url) %>%
column_to_rownames(., var = names(.)[1])W9.3 パイプ演算子 “%>%”
%>%はパイプ演算子と呼ばれ、データに対して複数の処理を連鎖的に行っていることを視覚的にわかりやすく記述するために導入されています。例えば、次の2つのコードは等価です。
result <- data %>%
function1() %>%
function2() %>%
function3()temp1 <- function1(data)
temp2 <- function2(temp1)
result <- function3(temp2)上記の例において%>%は次のような役割を担っています。
%>%の左側のオブジェクト(例えば、
data)を右側の関数(例えば、function1)に渡す関数の戻り値(ここでは
temp1に相当するもの)を右側の関数(例えば、function2)に渡す%>%が無い時点で処理の流れを止め、結果をresultに格納する
具体的には、%>%は左側のオブジェクトや関数の戻り値を右側の関数の第1引数に渡しています。このとき、受け渡されるオブジェクトは省略することができますが、.として明示的に書くことも可能です。したがって、上のコードは次とも等価です。%>%に慣れない内はこのように書くのも手でしょう。
result <- data %>%
function1(.) %>%
function2(.) %>%
function3(.)W9.4 複数の列に関数を適用する
複数の列に関数を適用するには、mutate(across())という関数を利用すると良いでしょう。mutate関数は本来、新しい列を作成したり既存の列を変更したりする際に使われる関数であり、単独でも頻繁に使用されますがacross関数と組み合わせることで、同じ処理を複数の列に対して一括に適用することもできます。次のコードはすべての列に対して正規化を施し、Anormというオブジェクトに格納するものです。
Anorm <- A %>%
mutate(across(everything(), ~ 1000000 * . / sum(.))) ここでは処置対象の列を指定する際に、everything関数を使用して”Aのすべての列を対象とする”と指示しています。その他に列を選択する際便利な補助関数として、“◯◯という文字列から始まる列”を選択するstarts_with関数や、“◯◯という文字列を含む列”を選択するcontains関数など多くの関数が用意されています。
処理内容を記述する第2引数の部分では、~という記号が使用されていますが、これは単に”後続の処理を適用してほしい”と意味しています。これは無名関数(他の言語では”ラムダ式”とも呼ばれます)を用いた書き方であり、簡単な処理に対して関数を別途定義する手間を省くためのテクニックとして割と頻繁に使用されます。少し冗長にはなりますが上記のコードは次の書き方と同じ意味です。
norm_func <- function(x) {
return(1000000 * x / sum(x))
}
Anorm <- A %>%
mutate(across(everything(), norm_func))
#' ---気になる人向け---
#' パイプ演算子内の関数の引数に関数をわたしたい場合、
#' 関数オブジェクトを渡さなければならなりません。
#' 下記のnorm_funcに()がついていないのはそのためです。
#' これは主にtidyverseのパイプ演算子をサポートする
#' パッケージ"magrittr"の仕様によるものです。W9.5 データの”縦持ち”と”横持ち”とは?
同じ情報を持つデータでも、その表現方法には”横持ち”と”縦持ち”の2つの形式があります。一般的に、横持ちのデータは人が見てわかりやすい形式であり、縦持ちのデータは計算機による処理に適した形式とされています。それでは、まずはざっと目でこれらの形式を確認してみましょう。
次に、おなじみの横持ちで表されたカウントデータを見てみます。
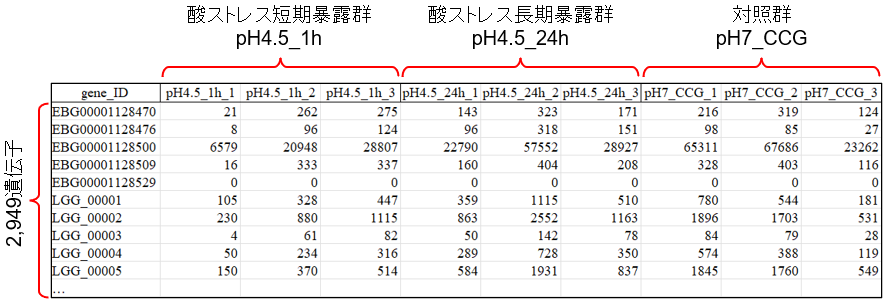
head(A)## pH4.5_1h_1 pH4.5_1h_2 pH4.5_1h_3 pH4.5_24h_1 pH4.5_24h_2
## EBG00001128470 21 262 275 143 323
## EBG00001128476 8 96 124 96 318
## EBG00001128500 6579 20948 28807 22790 57552
## EBG00001128509 16 333 337 160 404
## EBG00001128529 0 0 0 0 0
## LGG_00001 105 328 447 359 1115
## pH4.5_24h_3 pH7_CCG_1 pH7_CCG_2 pH7_CCG_3
## EBG00001128470 171 216 319 124
## EBG00001128476 151 98 85 27
## EBG00001128500 28927 65311 67686 23262
## EBG00001128509 208 328 403 116
## EBG00001128529 0 0 0 0
## LGG_00001 510 780 544 181一方、次は縦持ちに変換したデータです。
A %>%
rownames_to_column(var = "gene_ID") %>%
pivot_longer(cols = -gene_ID, names_to = "sample", values_to = "count") %>%
separate(sample, into = c("pH", "time", "replicate"), sep = "_") %>%
unite("pH_time", c("pH", "time"), sep = "_") %>%
head(A, n = 10)## # A tibble: 10 × 4
## gene_ID pH_time replicate count
## <chr> <chr> <chr> <dbl>
## 1 EBG00001128470 pH4.5_1h 1 21
## 2 EBG00001128470 pH4.5_1h 2 262
## 3 EBG00001128470 pH4.5_1h 3 275
## 4 EBG00001128470 pH4.5_24h 1 143
## 5 EBG00001128470 pH4.5_24h 2 323
## 6 EBG00001128470 pH4.5_24h 3 171
## 7 EBG00001128470 pH7_CCG 1 216
## 8 EBG00001128470 pH7_CCG 2 319
## 9 EBG00001128470 pH7_CCG 3 124
## 10 EBG00001128476 pH4.5_1h 1 8これらのデータを比較してみると、縦持ちのデータでは、列に含まれていた”pH4.5”や”pH7”という情報が、抽象化された”pH”という列名の中に格納されていることがわかります。同様に、列名の”1h”、“24h”や”CCG”という情報は”time”という列に、各反復に付けられた番号”1〜3”は”replicate”という列にまとめて格納されています。つまり、縦持ちのデータでは、1行にあたり1つの観測値(count)と観測条件(gene_ID、pH_time、replicate)が含まれる形式を持つようになります。
縦持ちに変換することによって処理の高速化、可視化の容易さなど、計算機目線のメリットも多く存在します。しかし殊解析においては、列名に隠れていた観測条件をデータの値として抽出し、その値に基づいて計算機が処理を変えることができるようになるという点が大きなメリットと言えるでしょう。
今回の場合、“酸ストレス短期暴露群(pH4.5_1h)”、“酸ストレス長期暴露群(pH4.5_24h)”、“対照群(pH7_CCG)の各3回の反復において平均、分散、dispersionの3つの値を算出することがゴールです。このような時にはpivot_longer関数とgroup_by関数の組み合わせが非常に有効です。具体的なやり方を次のW9.6で見ていきましょう。
W9.6 データを縦持ちに変換し、グループごとに処理を適用する
再度横持ちのデータから出発し、縦持ちへの変換とグループごとの処理に用いる関数を一つずつ見ていきましょう。
head(Anorm)## pH4.5_1h_1 pH4.5_1h_2 pH4.5_1h_3 pH4.5_24h_1 pH4.5_24h_2
## EBG00001128470 90.05339 311.6814 256.3264 152.3241 122.2947
## EBG00001128476 34.30605 114.2039 115.5799 102.2595 120.4016
## EBG00001128500 28212.44023 24920.2357 26850.8861 24275.9814 21790.4089
## EBG00001128509 68.61211 396.1447 314.1163 170.4325 152.9630
## EBG00001128529 0.00000 0.0000 0.0000 0.0000 0.0000
## LGG_00001 450.26694 390.1965 416.6469 382.4080 422.1627
## pH4.5_24h_3 pH7_CCG_1 pH7_CCG_2 pH7_CCG_3
## EBG00001128470 145.3073 90.68082 181.35634 217.56409
## EBG00001128476 128.3123 41.14223 48.32379 47.37283
## EBG00001128500 24580.7331 27418.77454 38480.51812 40814.32133
## EBG00001128509 176.7481 137.70051 229.11162 203.52770
## EBG00001128529 0.0000 0.00000 0.00000 0.00000
## LGG_00001 433.3728 327.45853 309.27226 317.57339列名を観察すると、“(pHの値)_(暴露した時間)_(反復数)”という形式で統一されていることがわかります。例えば最初のpHについて注目すると、“pH4.5_・・・”と”pH7_・・・“の2種類存在します。よって、これらをまとめて”pH”という名前の列を作って、その中の値として”pH4.5”と”pH7”のいずれかが格納されているようにするのが変換のゴールです。同様に、2番目の暴露した時間は”time”という列に、3番目の反復については”replicate”という列にまとめることにしましょう。また、肝心の観測値は”count”という列名に格納することにします。
縦持ちデータへの変換にはpivot_longer関数という便利なモジュールが用意されており、このように”_“などのデリミタで分けられた列名に対して特に柔軟な操作を可能にしています。cols = -gene_IDは”gene_IDという列を除く全ての列”という意味であることを踏まえて、次のようにデータを縦持ちに変数することができます。実際に縦持ちに変換できているか確認しましょう。
Anorm %>%
rownames_to_column(var = "gene_ID") %>%
pivot_longer(cols = -gene_ID, names_to = c("pH", "time", "replicate"), values_to = "count", names_sep = "_") %>%
head()## # A tibble: 6 × 5
## gene_ID pH time replicate count
## <chr> <chr> <chr> <chr> <dbl>
## 1 EBG00001128470 pH4.5 1h 1 90.1
## 2 EBG00001128470 pH4.5 1h 2 312.
## 3 EBG00001128470 pH4.5 1h 3 256.
## 4 EBG00001128470 pH4.5 24h 1 152.
## 5 EBG00001128470 pH4.5 24h 2 122.
## 6 EBG00001128470 pH4.5 24h 3 145.無事”pH”、“time”、“replicate”という名前の列を作り、条件を値になおすことができたようです。このまま次の解析に進んでも良いですが、3つの群の条件は”pH
+
time”と簡潔に表されるため、今のままではやや冗長に思えます。例えばG1は”pH4.5_1h”、G2は”pH4.5_24h”のよう表した方がわかりやすく、今後の解析も楽に進められそうです。unite関数で”pH_time”という名前の列を作成し、“pH”と”time”の列を一つの変数としてまとめそこに格納してみよましょう。
Anorm %>%
rownames_to_column(var = "gene_ID") %>%
pivot_longer(cols = -gene_ID, names_to = c("pH", "time", "replicate"), values_to = "count", names_sep = "_") %>%
unite(col = "pH_time", c("pH", "time"), sep = "_") %>%
head()## # A tibble: 6 × 4
## gene_ID pH_time replicate count
## <chr> <chr> <chr> <dbl>
## 1 EBG00001128470 pH4.5_1h 1 90.1
## 2 EBG00001128470 pH4.5_1h 2 312.
## 3 EBG00001128470 pH4.5_1h 3 256.
## 4 EBG00001128470 pH4.5_24h 1 152.
## 5 EBG00001128470 pH4.5_24h 2 122.
## 6 EBG00001128470 pH4.5_24h 3 145.以上で縦持ちのtidyなデータを用意することができました。次に各遺伝子の各群ごとで求めたい統計量を算出していきましょう。
一旦縦持ちになおしてしまえば、次のようにパイプ演算子内で処理したい部分をgroup_by関数とungroup関数で挟むだけで自動的にグループ分けして処理してくれます。今回は遺伝子のグループ(gene_ID列)と条件のグループ(pH_time列)ごとに処理したいので、group_by関数の引数にそれらの列名を指定します。次のコード内の”#
処理したい内容”は、gene_IDの値とpH_timeの値ごとにに処理されます。つまりreplicateの1〜3に対して各統計量が計算されるようになります。
Anorm %>%
rownames_to_column(var = "gene_ID") %>%
pivot_longer(cols = -gene_ID, names_to = c("pH", "time", "replicate"), values_to = "count", names_sep = "_") %>%
unite(col = "pH_time", c("pH", "time"), sep = "_") %>%
group_by(gene_ID, pH_time)
# 処理したい内容
ungroup()
head()W9.7 列やグループごと情報を1つの値に要約する
ある列やグループにはたいてい複数の値が入っています。これらの値を処理して、平均値といった1つの値に集約したい時はsummarise関数が有効です。“複数の値→1つの値”という処理がこの関数の大きな役目ですから、BaseRに標準装備されている関数の他に自前の関数を用いて集約させることも可能です。次のコードは各グループごとの平均M、分散V、dispersionのPhiを算出するコードですが、Phi = func_phi()
のように、先に読み込んだ関数を利用して処理を行っていることに注目してください。
Anorm %>%
rownames_to_column(var = "gene_ID") %>%
pivot_longer(cols = -gene_ID, names_to = c("pH", "time", "replicate"), values_to = "count", names_sep = "_") %>%
unite(col = "pH_time", c("pH", "time"), sep = "_") %>%
group_by(gene_ID, pH_time) %>%
summarize(
M = mean(count),
V = var(count),
Phi = func_phi(count)
) %>%
ungroup()## `summarise()` has grouped output by 'gene_ID'. You can override using the
## `.groups` argument.## # A tibble: 8,847 × 5
## gene_ID pH_time M V Phi
## <chr> <chr> <dbl> <dbl> <dbl>
## 1 EBG00001128470 pH4.5_1h 219. 13305. 0.272
## 2 EBG00001128470 pH4.5_24h 140. 247. 0.00545
## 3 EBG00001128470 pH7_CCG 163. 4272. 0.154
## 4 EBG00001128476 pH4.5_1h 88.0 2165. 0.268
## 5 EBG00001128476 pH4.5_24h 117. 178. 0.00449
## 6 EBG00001128476 pH7_CCG 45.6 15.2 -0.0146
## 7 EBG00001128500 pH4.5_1h 26661. 2736642. 0.00381
## 8 EBG00001128500 pH4.5_24h 23549. 2342809. 0.00418
## 9 EBG00001128500 pH7_CCG 35571. 51208247. 0.0404
## 10 EBG00001128509 pH4.5_1h 260. 29046. 0.427
## # ℹ 8,837 more rowsW9.8 データを横持ちになおす
縦持ち形式のデータが計算機による処理に適していることは先に見てきましたが、一方でヒトにとっては読みにくい形式と言えます。今後の解析をスムーズにすすめるためにも、最後にデータを横持ちになおすことにしましょう。pivot_wider関数を用います。pivot_wider関数はnames_ftomで指定された列に格納された値を列名へと変換する機能を提供しています。names_sep引数で指定されたデリミタを用いてvalues_from引数で指定された列名を結合して新たな列を作成し、values_from引数の各列の値をそれらの列に格納します。
Anorm %>%
rownames_to_column(var = "gene_ID") %>%
pivot_longer(cols = -gene_ID, names_to = c("pH", "time", "replicate"), values_to = "count", names_sep = "_") %>%
unite(col = "pH_time", c("pH", "time"), sep = "_") %>%
group_by(gene_ID, pH_time) %>%
summarize(
M = mean(count),
V = var(count),
Phi = func_phi(count)
) %>%
ungroup() %>%
pivot_wider(names_from = pH_time, values_from = c("M", "V","Phi"), names_sep = "_")## `summarise()` has grouped output by 'gene_ID'. You can override using the
## `.groups` argument.## # A tibble: 2,949 × 10
## gene_ID M_pH4.5_1h M_pH4.5_24h M_pH7_CCG V_pH4.5_1h V_pH4.5_24h V_pH7_CCG
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 EBG0000112… 219. 140. 163. 13305. 247. 4.27e3
## 2 EBG0000112… 88.0 117. 45.6 2165. 178. 1.52e1
## 3 EBG0000112… 26661. 23549. 35571. 2736642. 2342809. 5.12e7
## 4 EBG0000112… 260. 167. 190. 29046. 152. 2.22e3
## 5 EBG0000112… 0 0 0 0 0 0
## 6 LGG_00001 419. 413. 318. 906. 717. 8.29e1
## 7 LGG_00002 1024. 958. 899. 1089. 1242. 8.23e3
## 8 LGG_00003 55.4 57.8 43.1 1100. 54.4 5.05e1
## 9 LGG_00004 262. 294. 223. 1795. 270. 2.65e2
## 10 LGG_00005 521. 688. 913. 11616. 3372. 1.47e4
## # ℹ 2,939 more rows
## # ℹ 3 more variables: Phi_pH4.5_1h <dbl>, Phi_pH4.5_24h <dbl>,
## # Phi_pH7_CCG <dbl>W9.9 列の名前を変更する
現在、各実験条件は”(pHの値)_(暴露した時間)“という形式で表されていますが、これをさらに簡潔に記述できるように”G1”、“G2”、“G3”という形に列名を変更しておきましょう。この処理のメリットは、もちろんデータの視認性の向上もありますが、tidyverseでは「末尾がG1で終わる列のMとPhiの値を〇〇して・・・」のように列名を指定して解析を行う場合が多いため、コードを書く際の手間を減らしミスを少なくする、という面でも大きいと言えます。
列名を変更する最もシンプルな方法はrename関数を用いるものです。しかしこの方法で一つ一つ名前を変えていくのは手間ですし、ミスの温床になり得ます。今回のように特定の条件を満たす列名を一括で変更したいときは、rename_with関数を用いるのが有効です。以下のコードでは、末尾が”pH4.5_1h”、“_pH4.5_24h”、“_pH7_CCG”で終わる列をそれぞれ一括で選択し、Base-Rに含まれるgsub関数により正規表現を用いて変更を行っています。
Anorm %>%
rownames_to_column(var = "gene_ID") %>%
pivot_longer(cols = -gene_ID, names_to = c("pH", "time", "replicate"), values_to = "count", names_sep = "_") %>%
unite(col = "pH_time", c("pH", "time"), sep = "_") %>%
group_by(gene_ID, pH_time) %>%
summarize(
M = mean(count),
V = var(count),
Phi = func_phi(count)
) %>%
ungroup() %>%
pivot_wider(names_from = pH_time, values_from = c("M", "V","Phi"), names_sep = "_") %>%
rename_with(~gsub("_pH4.5_1h$", "_G1", .), ends_with("_pH4.5_1h")) %>%
rename_with(~gsub("_pH4.5_24h$", "_G2", .), ends_with("_pH4.5_24h")) %>%
rename_with(~gsub("_pH7_CCG$", "_G3", .), ends_with("_pH7_CCG")) ## `summarise()` has grouped output by 'gene_ID'. You can override using the
## `.groups` argument.## # A tibble: 2,949 × 10
## gene_ID M_G1 M_G2 M_G3 V_G1 V_G2 V_G3 Phi_G1 Phi_G2 Phi_G3
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 EBG00001… 2.19e2 1.40e2 1.63e2 1.33e4 2.47e2 4.27e3 2.72e-1 5.45e-3 1.54e-1
## 2 EBG00001… 8.80e1 1.17e2 4.56e1 2.17e3 1.78e2 1.52e1 2.68e-1 4.49e-3 -1.46e-2
## 3 EBG00001… 2.67e4 2.35e4 3.56e4 2.74e6 2.34e6 5.12e7 3.81e-3 4.18e-3 4.04e-2
## 4 EBG00001… 2.60e2 1.67e2 1.90e2 2.90e4 1.52e2 2.22e3 4.27e-1 -5.37e-4 5.63e-2
## 5 EBG00001… 0 0 0 0 0 0 0 0 0
## 6 LGG_00001 4.19e2 4.13e2 3.18e2 9.06e2 7.17e2 8.29e1 2.78e-3 1.79e-3 -2.32e-3
## 7 LGG_00002 1.02e3 9.58e2 8.99e2 1.09e3 1.24e3 8.23e3 6.18e-5 3.09e-4 9.08e-3
## 8 LGG_00003 5.54e1 5.78e1 4.31e1 1.10e3 5.44e1 5.05e1 3.41e-1 -1.01e-3 3.98e-3
## 9 LGG_00004 2.62e2 2.94e2 2.23e2 1.80e3 2.70e2 2.65e2 2.23e-2 -2.73e-4 8.35e-4
## 10 LGG_00005 5.21e2 6.88e2 9.13e2 1.16e4 3.37e3 1.47e4 4.09e-2 5.67e-3 1.65e-2
## # ℹ 2,939 more rows上のコードで一旦~を用いて無名関数を置いてgsub関数を呼び出している点が気になった人がいるかもしれません。W9.4でも同様な書き方をしていますが気になる人向けに説明すると、この理由はパイプ演算子内の関数の引数に関数を渡したいという時、関数オブジェクトの形で呼び出す必要があるのですが(つまり、gsubのみで呼び出すのが記法としては正しい)、それではgsub("_pH4.5_1h$", "_G1", .)のように“どのように文字列の変更を行うか”を引数で指定することができません。引数をとれるgsub(…)の形で関数を呼び出すために、無名関数と.を用いてrename_with関数に渡している、というわけです。
W9.10 まとめ
以上の説明を踏まえ、W2で示したコードをtidyverse流で記述した最終的なコードは次のようになります。
library(tidyverse)
source_url <- "https://www.iu.a.u-tokyo.ac.jp/kadota/book/JSLAB21_func.R"
input_file_url <- "https://www.iu.a.u-tokyo.ac.jp/kadota/book/JSLAB18.csv"
source(source_url)
A <- read_csv(input_file_url) %>%
column_to_rownames(., var = names(.)[1])
# 正規化
Anorm <- A %>%
mutate(across(everything(), ~ 1000000 * . / sum(.)))
# 各群の統計量を算出
result <- Anorm %>%
rownames_to_column(var = "gene_ID") %>%
pivot_longer(cols = -gene_ID, names_to = c("pH", "time", "replicate"), values_to = "count", names_sep = "_") %>%
unite(col = "pH_time", c("pH", "time"), sep = "_") %>%
group_by(gene_ID, pH_time) %>%
summarize(
M = mean(count),
V = var(count),
Phi = func_phi(count)
) %>%
ungroup() %>%
pivot_wider(names_from = pH_time, values_from = c(M, V, Phi), names_sep = "_") %>%
rename_with(~gsub("_pH4.5_1h$", "_G1", .), ends_with("_pH4.5_1h")) %>%
rename_with(~gsub("_pH4.5_24h$", "_G2", .), ends_with("_pH4.5_24h")) %>%
rename_with(~gsub("_pH7_CCG$", "_G3", .), ends_with("_pH7_CCG"))G1群のみの\(\varPhi\) > 0を満たす経験分布 (W10)
W10.1 列の選択
列を選択して抽出するためには、select関数を使用します。コードの中で単に列名を指定することも可能ですが、先に登場したstarts_with関数やends_with関数などの補助関数と組み合わせて使用することもできます。また、特定の列を除外する場合は、列名や列を取得する補助関数の前に-を付けるだけでその列を除外した結果を得ることもできます。例えば次のコードは、M_G1とPhi_G1を除いたすべての列を表示しています。
result %>%
select(-M_G1, -Phi_G1)## # A tibble: 2,949 × 8
## gene_ID M_G2 M_G3 V_G1 V_G2 V_G3 Phi_G2 Phi_G3
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 EBG00001128470 140. 163. 13305. 247. 4.27e3 5.45e-3 1.54e-1
## 2 EBG00001128476 117. 45.6 2165. 178. 1.52e1 4.49e-3 -1.46e-2
## 3 EBG00001128500 23549. 35571. 2736642. 2342809. 5.12e7 4.18e-3 4.04e-2
## 4 EBG00001128509 167. 190. 29046. 152. 2.22e3 -5.37e-4 5.63e-2
## 5 EBG00001128529 0 0 0 0 0 0 0
## 6 LGG_00001 413. 318. 906. 717. 8.29e1 1.79e-3 -2.32e-3
## 7 LGG_00002 958. 899. 1089. 1242. 8.23e3 3.09e-4 9.08e-3
## 8 LGG_00003 57.8 43.1 1100. 54.4 5.05e1 -1.01e-3 3.98e-3
## 9 LGG_00004 294. 223. 1795. 270. 2.65e2 -2.73e-4 8.35e-4
## 10 LGG_00005 688. 913. 11616. 3372. 1.47e4 5.67e-3 1.65e-2
## # ℹ 2,939 more rowsW10.2 行の選択
特定の条件を満たす行の選択と抽出には、filter関数を使用します。複雑な条件を指定したい場合、<(より小さい)や、==(等しい)などの比較演算子や、OR演算子|、AND演算子&といった論理演算子を組み合わせて表現できます。
select関数とfilter関数は、tidyverseを用いてデータを操作する際に頻繁に使用します。例えば遺伝子名と各群における統計量が格納されているresultから末尾が”G2”で終わる列を抽出し、その中でPhiが0より大きく、平均が50以下という条件を満たす遺伝子名を抽出するには、次のように記述します。
result %>%
select(gene_ID, ends_with("G2")) %>%
filter(Phi_G2 > 0 & M_G2 <= 50) %>%
select(gene_ID)## # A tibble: 292 × 1
## gene_ID
## <chr>
## 1 LGG_00008
## 2 LGG_00010
## 3 LGG_00018
## 4 LGG_00023
## 5 LGG_00033
## 6 LGG_00046
## 7 LGG_00065
## 8 LGG_00072
## 9 LGG_00081
## 10 LGG_00084
## # ℹ 282 more rowsW10.3 まとめ
以上の説明を踏まえ、W4.2で示したコードをtidyverse流で記述した最終的なコードは次のようになります。
sub_G1_M_Phi <- result %>%
select(M_G1, Phi_G1) %>%
filter(Phi_G1 > 0)
head(sub_G1_M_Phi)## # A tibble: 6 × 2
## M_G1 Phi_G1
## <dbl> <dbl>
## 1 219. 0.272
## 2 88.0 0.268
## 3 26661. 0.00381
## 4 260. 0.427
## 5 419. 0.00278
## 6 1024. 0.0000618乱数を生成 (W11)
W11.1 データからサンプリングする
データから行をサンプリングするには、slice_sample関数を使用します。BaseRのsample関数と同様に、replace引数をTRUEに指定することで復元抽出も可能です。
W11.2 1行ずつ処理を適用する
先に見てきたgroup_by関数は、列を指定することでその値を基にグループ分けして処理を行ってくれるものでした。それに対して、rowwise関数を適用すると、以降の一つ一つの行を個別のグループとして処理を行ってくれます。使い方もgroup_by関数と同様に、行ごとに行ってほしい処理をrowwise()とungroup()で挟むだけです。
rowwise関数を適用するとしないとでは得られる結果がかなり異なってしまいます。rowwise関数の役割を理解するために、rowwise関数を使用しなかった場合のコードの挙動を見ていきましょう。
G_sim <- 4
n_sim <- 5
set.seed(2023)
sub_G1_M_Phi %>%
slice_sample(n = G_sim, replace = TRUE) %>%
mutate(rep = list(rnbinom(n = n_sim, mu = .[["M_G1"]], size = 1 / .[["Phi_G1"]]))) %>%
unnest_wider(col = rep, names_sep = "_") %>%
mutate(gene_ID = paste0("gene", 1:nrow(.))) %>%
column_to_rownames("gene_ID") %>%
head()## M_G1 Phi_G1 rep_1 rep_2 rep_3 rep_4 rep_5
## gene1 875.46580 0.22292266 223 47 166 89 1038
## gene2 60.89932 0.16477002 223 47 166 89 1038
## gene3 274.83665 0.11164579 223 47 166 89 1038
## gene4 89.63483 0.04881805 223 47 166 89 1038上記のように、rep_1からrep_5の各列で延々と同じ値が繰り返されるという結果になりました。これはどういうことでしょうか。実は3行目のrnbinom関数の仕様による問題が起こっています。
上記のコードでは、rnbinom関数のmuとsize引数に要素数4(=
G_sim)の”M_G1”と”Phi_G1”が渡されますが、生成される乱数の個数はあくまで引数に指定したn個のみのようです。以下の例から、引数に要素数5のベクトルを渡しても整数を一つ渡しても、生成される乱数の個数は、n引数で指定した同じ3つであることを確認してください。
set.seed(2023)
rnbinom(n = 3, mu =5, size = 8)## [1] 4 2 2set.seed(2023)
# muとsizeに要素数5のベクトルを渡してみる
rnbinom(n = 3, mu = c(5, 3, 4, 9, 3), size = c(8, 2, 5, 1, 4))## [1] 4 5 7このようにrowwise関数を適用しない場合、rnbinom関数の引数にベクトルが渡され、関数による処理が1回だけ行われることになります。しかしその結果生成されるのは、あくまで要素数n個のベクトルです。そのベクトルが各行のrepという列に一様にコピーされることが原因で同じ値が生成されたように見えるというわけです。
rnbinom関数の引数に渡したいものは、あくまで各行における”M_G1”や”Phi_G1”といった列のひとつの値です。列をベクトルとしてまるごと引数に渡すのではなく、各行ごとに列の値を取り出して処理に渡したい場合に、rowwise関数が有効であることがわかるでしょう。
W11.3 ネストされた値を行方向に展開する
data.frame内の値にリストやベクトルを格納できる様に、tibbleの値にもリストやベクトルを格納することができます。以下の例では、各行のMとPhiをrnbinom関数に渡して得た乱数のベクトルがrepという列に格納されています。
G_sim <- 4
n_sim <- 5
set.seed(2023)
sub_G1_M_Phi %>%
slice_sample(n = G_sim, replace = TRUE) %>%
rowwise() %>%
mutate(rep = list(rnbinom(n = n_sim, mu = .[["M_G1"]], size = 1 / .[["Phi_G1"]]))) %>%
ungroup()## # A tibble: 4 × 3
## M_G1 Phi_G1 rep
## <dbl> <dbl> <list>
## 1 875. 0.223 <dbl [5]>
## 2 60.9 0.165 <dbl [5]>
## 3 275. 0.112 <dbl [5]>
## 4 89.6 0.0488 <dbl [5]>これらのベクトルを横方向に展開するために、unnest_wider関数を用いることができます。上の例ではひとつの値に格納されていた要素数5のベクトルが、下の例で行方向に一つずつ展開されていることを確認してください。
G_sim <- 4
n_sim <- 5
set.seed(2023)
sub_G1_M_Phi %>%
slice_sample(n = G_sim, replace = TRUE) %>%
rowwise() %>%
mutate(rep = list(rnbinom(n = n_sim, mu = .[["M_G1"]], size = 1 / .[["Phi_G1"]]))) %>%
ungroup() %>%
unnest_wider(col = rep, names_sep = "_")## # A tibble: 4 × 7
## M_G1 Phi_G1 rep_1 rep_2 rep_3 rep_4 rep_5
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 875. 0.223 223 47 166 89 1038
## 2 60.9 0.165 947 84 213 88 704
## 3 275. 0.112 1129 43 136 73 733
## 4 89.6 0.0488 1258 68 538 101 1022W11.4 まとめ
以上の説明を踏まえ、W4.6で示したコードをtidyverse流で記述した最終的なコードは次のようになります。
G_sim <- 4
n_sim <- 5
set.seed(2023)
simdata <- sub_G1_M_Phi %>%
slice_sample(n = G_sim, replace = TRUE) %>%
rowwise() %>%
mutate(rep = list(rnbinom(n = n_sim, mu = .[["M_G1"]], size = 1 / .[["Phi_G1"]]))) %>%
ungroup() %>%
unnest_wider(col = rep, names_sep = "_") %>%
mutate(gene_ID = paste0("gene", 1:nrow(.))) %>%
column_to_rownames("gene_ID") %>%
select(-"M_G1", -"Phi_G1")
simdata## rep_1 rep_2 rep_3 rep_4 rep_5
## gene1 223 47 166 89 1038
## gene2 947 84 213 88 704
## gene3 1129 43 136 73 733
## gene4 1258 68 538 101 1022遺伝子数10000のデータ生成 (W12)
W4.10に示したコードをtidyverse流に書くと次のようになります。G1群の平均とdispersionが格納されたオブジェクトsub_G1_M_Phiから10000行復元抽出し、それらをパラメータとして乱数を5個生成し行方向に展開することですべてがnonDEGである場合のシミュレーションデータとしています。実行した結果から、W4.10と同様に10000行(=遺伝子数)、5列(=反復数)のデータが生成されていることを確認してください。
G_sim <- 10000
n_sim <- 5
set.seed(2023)
simdata <- sub_G1_M_Phi %>%
slice_sample(n = G_sim, replace = TRUE) %>%
rowwise() %>%
mutate(rep = list(rnbinom(n = n_sim, mu = .[["M_G1"]], size = 1 / .[["Phi_G1"]]))) %>%
unnest_wider(col = rep, names_sep = "_") %>%
mutate(gene_ID = paste0("gene", 1:nrow(.))) %>%
column_to_rownames("gene_ID") %>%
select(-"M_G1", -"Phi_G1")
dim(simdata)## [1] 10000 5DEGありのデータ生成 (W13)
W13.1 \(\varPhi\) > 0を満たす経験分布を得る
W7.1に示したコードをtidyverse流に書くと次のようになります。G1〜G3のすべての群から、乱数生成のパラメータに使用するMとPhiをデータから抽出し、縦持ちに変換してPhiが0より大きいものを抽出、そして縦持ちのままsub_M_Phiに格納しています。sub_M_Phiの行数がW7.1の結果と同じであることを確認してください。このような処理において、tidyverseの可読性の高さや縦持ちの便利さが際立つと言えるでしょう。
sub_M_Phi <- result %>%
select(-starts_with("V")) %>%
pivot_longer(cols = c(starts_with("M"), starts_with("Phi")), names_to = c(".value", "group"), names_sep = "_") %>%
filter(Phi > 0)
nrow(sub_M_Phi)## [1] 6026W13.2 全てがnonDEGの数値行列を生成
W7.2に示したコードをtidyverse流に書くと次のようになります。W13.1で得たsub_G1_M_Phiから10000行を反復抽出を許してサンプリングし、それらの値をパラメータとし5つの乱数を生成することで全てnonDEGのシミュレーションデータとしています。
G_sim <- 10000
nk <- c(3, 3)
set.seed(2023)
simdata <- sub_G1_M_Phi %>%
slice_sample(n = G_sim, replace = TRUE) %>%
rowwise() %>%
mutate(G1 = list(rnbinom(n = nk[1], mu = .data[["M_G1"]], size = 1 / .data[["Phi_G1"]])),
G2 = list(rnbinom(n = nk[2], mu = .data[["M_G1"]], size = 1 / .data[["Phi_G1"]]))) %>%
unnest_wider(col = G1, names_sep = "_") %>%
unnest_wider(col = G2, names_sep = "_") %>%
select(-"M_G1", -"Phi_G1")
head(simdata)## # A tibble: 6 × 6
## G1_1 G1_2 G1_3 G2_1 G2_2 G2_3
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 997 530 814 512 452 1033
## 2 103 78 75 37 47 30
## 3 306 136 355 186 327 416
## 4 66 118 115 86 79 92
## 5 39 8 10 7 2 12
## 6 127 174 133 161 181 162W13.3 DEGの導入
W7.5に示したコードをtidyverse流に書くと次のようになります。mutate関数を用いて、nonDEGで生成したシミュレーションデータsimdataから、G1で高発現するDEGを1〜2250行目、G2で高発現するDEGを2251〜2500行目として導入しています。
G_sim <- 10000
nk <- c(3, 3)
PDEG <- 0.25
P1 <- 0.9
FC <- 4simdata_DEG <- simdata %>%
mutate(across(starts_with("G1"), ~ ifelse(row_number() <= G_sim * PDEG * P1, . * FC, .))) %>%
mutate(across(starts_with("G2"), ~ ifelse(row_number() > G_sim * PDEG * P1 & row_number() <= G_sim * PDEG, . * FC, .)))
write.csv(x=simdata_DEG, file="JSLAB21_w7.5_tidyverse.csv")W13.4 ヒストグラムによるDEGありシミュレーションデータの確認
W7.6に示したコードをtidyverse流に書くと次のようになります。tidyverseの記法によって生成したDEGありのシミュレーションデータのヒストグラムと、W7.6のヒストグラムが同様の形状を示していることを確認してください。
M <- simdata_DEG %>%
rowwise() %>%
mutate(
M_G1 = mean(c_across(starts_with("G1"))),
M_G2 = mean(c_across(starts_with("G2")))) %>%
ungroup() %>%
select(starts_with("M")) %>%
mutate(logratio = log2(M_G2/M_G1))axis_range <- c(-4, 4)
g <- ggplot(M, aes(x=logratio)) +
geom_histogram() +
coord_cartesian(xlim=axis_range)
plot(g)