以前の研究から
回折限界を超えた位置測定:量子気体から生体分子まで
背景:物理法則で決まる原理的限界により光の波長よりも小さい対象物は見えないと考えられてきました。この位置分解能の限界ー回折限界ーはおよそ光が関係するあらゆる分野における長年の課題でありました。特に、近年冷却原子系で実現した量子気体顕微鏡においては回折限界が要求する高い信号雑音比のために測定が破壊的になってしまうという制約がありました。また、2014年のノーベル化学賞の対象にもなった生命科学における超解像度蛍光顕微鏡においては膨大な撮像回数が必要となってしまうために時間分解能が大きな制約でした。
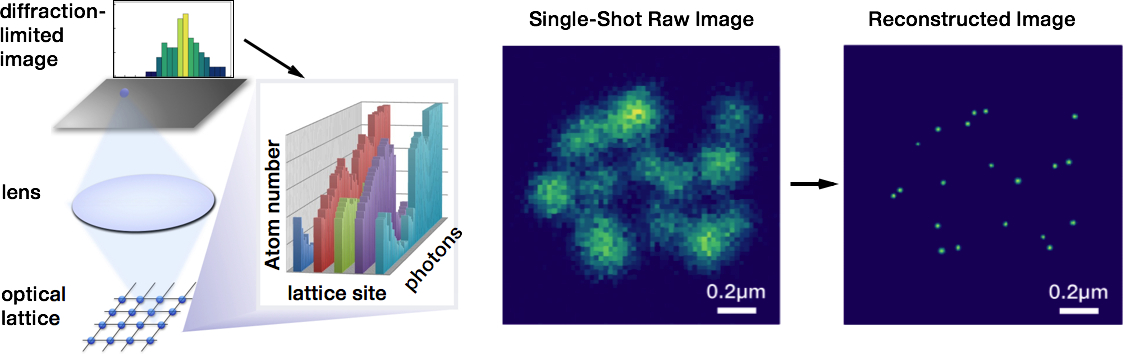
研究:我々は、回折限界を超えた分解能で原子や分子の位置を測定するための理論的枠組みと計算手法を確立しました。特に、光格子系において量子測定理論を用いて多体波動関数の収縮を追跡することで、原子位置が高フィデリティーで決定できることを示しました。これにより少数光子・非共鳴散乱光を用いた非破壊なシングルサイト測定が行える可能性を指摘しました。さらに、理論を古典系にも拡張し超解像蛍光顕微鏡に応用することで、時間分解能の理論限界を達成できる解析手法を構築する事に成功しました。
[光格子系の超解像非破壊測定] PRL 2015
[連続空間上の超解像測定手法] Opt. Lett. 2016
非平衡統計力学 (古典系及び量子開放系)
背景:熱平衡状態にあるマクロな物理系は従来の熱・統計力学により精緻に記述されます。一方で、平衡から遠く離れた物理系の基礎理論を模索する試みは物理学における長年の課題でした。近年、Jarzynski等式やゆらぎの定理と呼ばれる非平衡等式の発見に端を発して、微小な非平衡系における統計力学が古典・量子系双方において活発に研究されています。特に、測定やフィードバック制御を非平衡統計力学の枠組みに取り入れた"情報熱力学"と呼ばれる分野が近年確立されつつあります。
研究:ゆらぎの定理を誤差の無い理想的なフィードバック制御を行った場合にも拡張する事で、フィードバック制御で取り出せる仕事の達成可能な上限を導きました。また、量子開放系において非平衡統計力学の枠組みを構築することで、量子測定とフィードバック制御を行った場合に一般化されたゆらぎの定理が成立する事を示しました。
[古典系] PRE 2014, PRE 2021
[量子開放系] PRA 2016