spin orbit coupling and SU(2) gauge
スピン軌道相互作用（spin orbit coupling =SOC)とは 軌道角運動量Lとスピン角運動量Sが -ζL・Sの形で混成する相互作用で 周期律表のうしろのほうにある3d/4d/5d, 4f/5fなどの原子から構成される系でしばしば重要な役割を果たします. これらの電子系は原子に局在した電子軌道をもつので, SOCによって各原子において 複数の異なった角運動量とスピンをもった軌道がまじりあいJ=L+Sの新たな角運動量を持った軌道を構成します. 一番シンプルなパターンは, 時間反転対称性に守られたKramers縮退と呼ばれる２重縮退のある軌道が構成され, 他の軌道に比べて エネルギー的に分離しているためにこの軌道だけを考えればよい場合です. 一般的なハミルトニアンの形は, tight binding モデルの範疇では以下のように表せます.



ここでのスピン↑,↓は, SOCによって角運動量がまじりあったKramers二重項の二つの準位の自由度をあらわします. 物質の詳細に依存するものの, 実際にはこのスピンは磁化と結び付けられます. SOCによって電子の実空間での運動と磁性（スピン）が混じるということは, 電子がある原子（サイト）から 隣の原子に飛び移る際に, スピンの向きを変える効果が生じるということを意味します. λはまさにそのような項になっています. これが通常のスピンの向きを変えない飛び移り項(t)とあわさって合成されると上下スピンの電子を２成分として 2x2の行列で表される形に変換されます. この2x2行列は簡単な計算で U_ijのようにexpの肩に2x2行列が載ったユニタリ回転行列＝SU(2）ゲージとして表現されます.
Antisymmetric SOC Mott insulator
[Kawano, Hotta Phys. Rev. B, 107 045123 (2023), Makuta, Hotta, arXiv 2304.08199 (2023)]
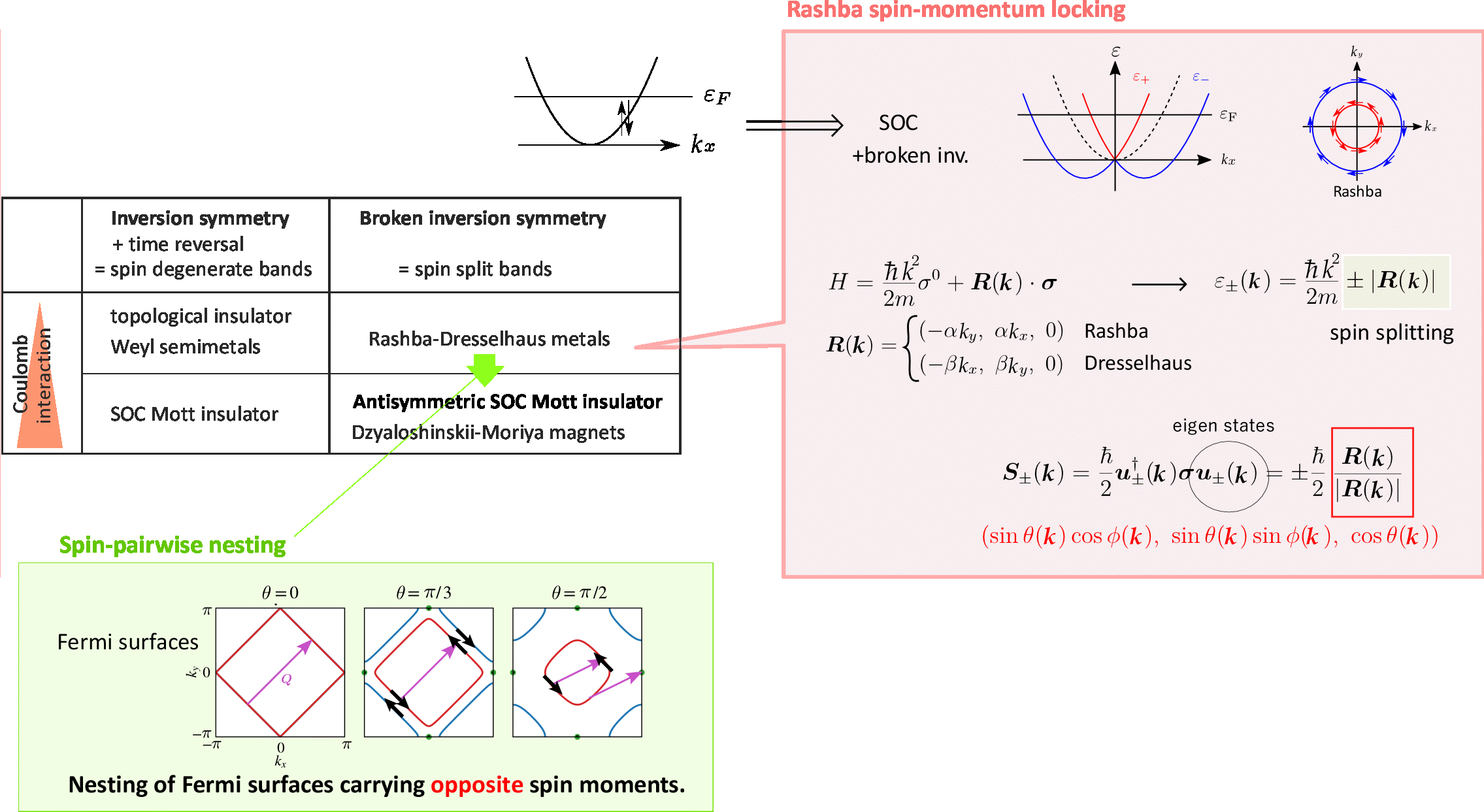
まずH_kinだけを単純に対角化してバンドを描き, そのうえで更にそこに相互作用が加わった場合を想定しましょう. ここで同じSOCハミルトニアンに対しても, 空間反転対称性(inversion symmetry)の有無とクーロン相互作用（電子相関）の大小に応じて物理が変わります. まずバンドについて： SOCのもとでも, 空間反転対称性と時間反転対称性が合わさると, ``上下"スピンのバンドが縮退します. ところがもし空間反転対称性が破れると バンドは spin splittingを起こします. 通常, SOCがない場合は, バンドは上下スピンで縮退しますが, 各バンドが運ぶスピンの向きは波数kに 依らず一様ですが SOCがあると, スピンがいい量子数とはならなくなるので, 各k点でspin splitした バンドのペアの固有状態は反対方向を向いたスピンのペアを構成します.
実際に反転対称性が破れた場合について連続体のHamilonianで簡単に説明できる有名な例が 相互作用が弱い半導体のRashba系のspin momentum lockingです. この場合, ハミルトニアンの形が上述の局在性が強いd,f軌道の場合とはちょっと異なりますが本質はあまり変わりません. （連続極限で注目するparabollicなバンドの底の近く部分を見てると思ってもよい） ここではR(k)というベクトルがSOCを表します. このR(k)は ｋに依存して向きを変える一種のZeeman磁場として働き, バンドを分裂させる. その結果, 各k点で分裂したバンドは R(k)と平行、反平行の向きにスピンをもっており フェルミ面に沿ってこれを眺めるとバンドが運ぶスピンの向きがぐるぐる回転していて k*pは一定に見えるのでこれを spin momentum lockingと呼ばれます. 実際にはもう少し複雑なバンドや相互作用などのもと, ｋ空間でスピンはいろいろなテクスチャを描きます.
このようなspin split bandにクーロン相互作用Ｕを加えると, あるＵｃで 対称性を破る相転移を起こして スピン密度波（ＳＤＷ）が生じます. この相転移は フェルミ面が spin-pairwise nestingを起こして生じることが最近わかりました(Kawano-Hotta 2023). この現象は逆向きのスピンを運ぶフェルミ面をさし渡しするベクトルQに対して スピン感受率（SOCがある場合３x３の行列） が発散する不安定性によって起こる磁気転移です（必ずしも金属絶縁体転移にはならない）. ちなみにspin splittingがない場合はふつうのスピンに依存しないnestingが起こります.


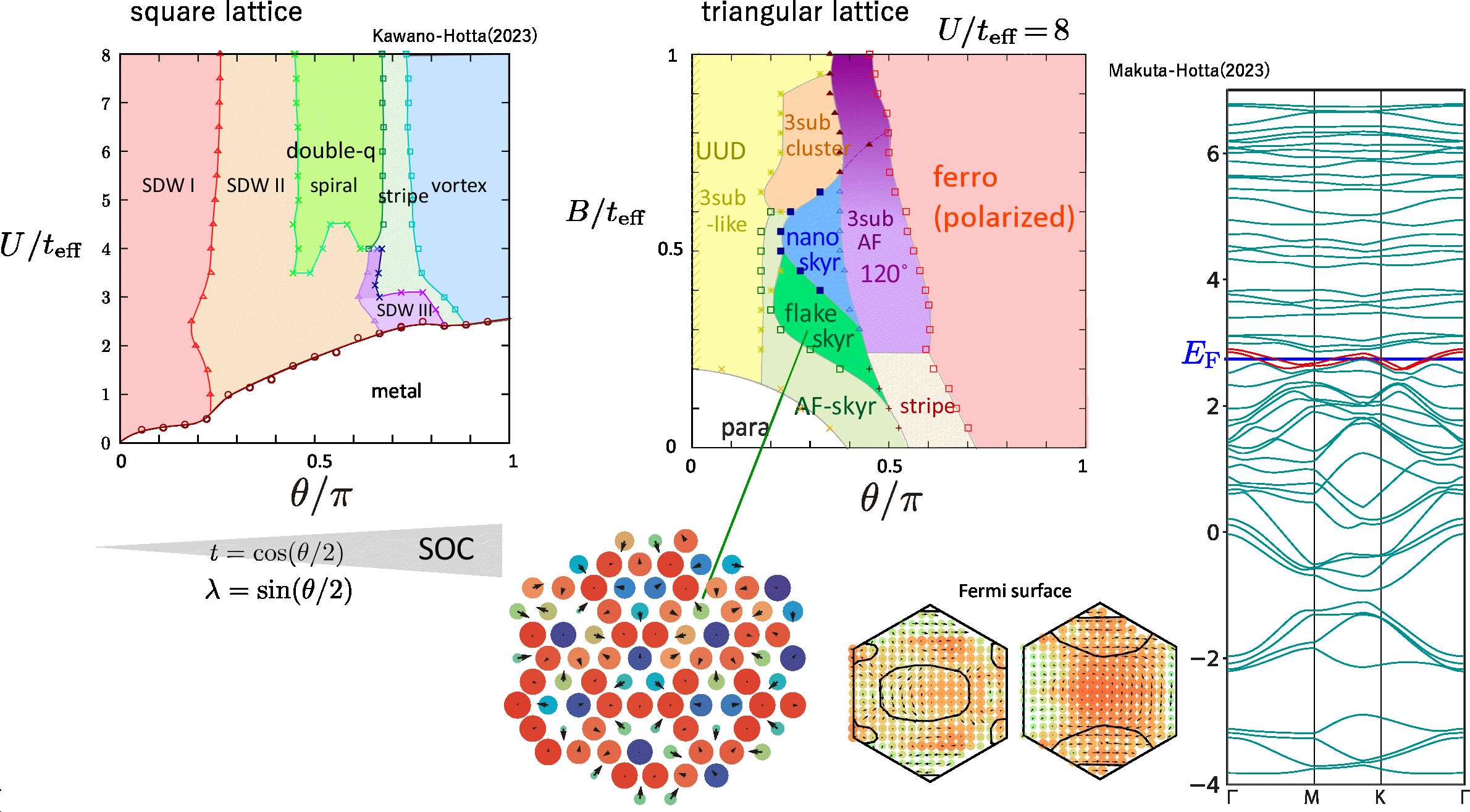
さて, こうしてできた磁気秩序はしばしば長波長（波数Qに対応）のincommensurate(格子と非整合)な構造をもちます. 正方格子のRashba型の 更に相互作用Uが増大しても磁気構造はあまり変わりません. 正方格子と三角格子のhalf-fillingのRashba SOCの場合の 相図を示しておきます. λとtがだいたい同じくらいの大きさの領域 (θ=π/2付近）で double-q spiral や skyrとかかれている相は skyrmion相です. Skyrmion相は一般に, 実空間でゆるやかにスピンが上から下に変化する 古典的にトポロジカルなスピン構造を指し, 従来は古典スピン模型で古典計算 （スピンの大きさSが大きく, 絶縁体系で正当化されるモデル）や現象論によって 主に議論されていました. ここで得られた相図はハバードモデルで得られたものなので, 電子スピンが実空間でskyrmion構造をもち, かつ 電子がフェルミ面をもって金属としてふるまいながらも ｋ空間で spin textureをもち かつ バンド（赤くマークされたバンドは chern# 2, -1をもつ） Chern数という量子的にトポロジカルな性質ももつ, skyrmionとして初めての例となっています.