Numerical Methods
We here introduce some pieces of our paper on numerical methods.
Grand canonoical approach
[Hotta-Shibata PRB86 041108 (2012) , Hotta-Nishimoto-Shibata PRB 87115128 (2013) ]
It seems quite usual to consider that the nature of the system is determined solely by the Hamiltonian, and modifying the Hamiltonian means changing the state itself. However, it was once pointed out by Nishino (at around 2010) that if we consider a warped space consisting of real-imaginary time axes, and trying to make a imaginary time evolution without changing the profile of the wave function, one needs to modify the Hamiltonian. This idea has developed since than and nowadays accepted as a protocol called "sine square deformation" (SSD). The grand canonical approach made use of this protocol to get rid of the finite size effect in the quantum many body calculation.
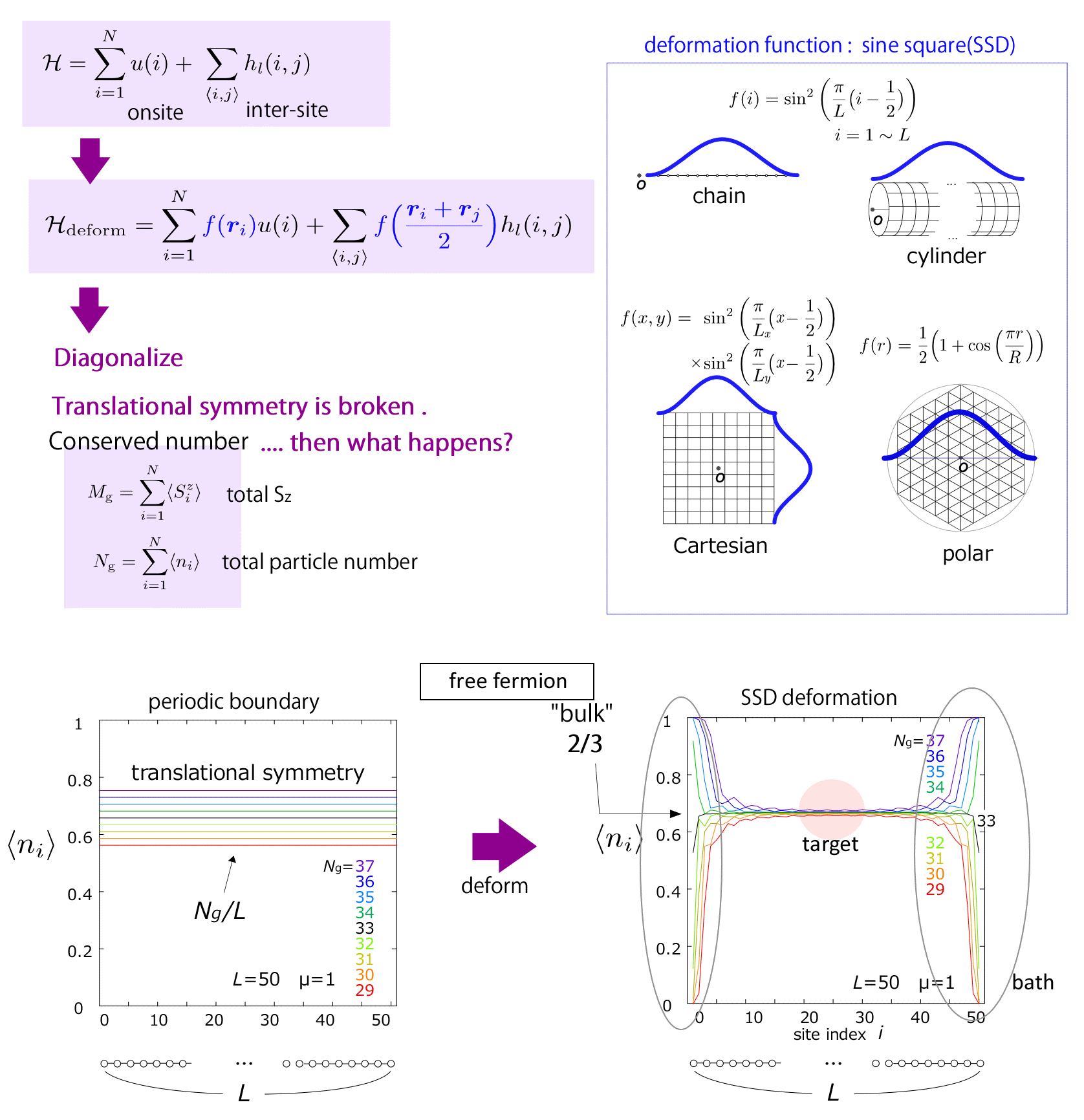
The key ingredient of this analysis is to deform the Hamiltonian in real space. For the uniform (original) Hamiltonian with periodic boundary condition (PBC) the expectation values of the physical quantities of the ground state also remains translationally invariant. In isolated quantum systems, there are several conserved quantities such as particle number Ng and magnetization Mg. The expectation values of the particle density and the magnetization density per site then becomes Ng/N and Mg/N, respectively, where N is the system size. This is also valid even if we put the grand potential term including the chemical potential μ (or magnetic field h conjugate to the magnetization).
Once we place the SSD to the Hamiltonian, the translational symmetry is broken. This SSD function takes the form of a single wavelength, with maximum at the center of the system and zero at both edges. The energy scale of the Hamiltonian is modified to scale smoothly down from order-1 at the center toward 0 at the edges.
In the figure we show the case of free fermion in one dimension. For the periodic boundary the particle density is uniform and shifts according to the value of Ng. After SSD, the particle distribution in space is redistributed in a nonuniform manner. When varying Ng the particle density at the system edge drastically changes, whereas at the center they remain almost unchanged. The value at the center corresponds to the ideal particle number conjugate to the given value of μ for N=∞. This means that by extracting the value at the center one could evaluate the proper particle density for a given μ. Indeed, for one-dimension, the accuracy of the obtained value for the system as small as N=10-50 is about 10-4 against the exact solution in the bulk limit.
In usual DMRG calculations, we always examine several different sizes, N=50,100, 150, ... and perform the size scaling against 1/N to obtain the value at N=∞ . However, in this analysis we no longer need a size scaling.
Another advantage is that, one can deal with the incommensurate state with long periodicity, such as spiral state. In usual open or periodic boundaries one needs to adopt N to be multiples of the periodicity m of the state we are focusing. If m varies with system parameters, the calculation becomes a mess. We showed in our first paper that for the J1J2model in one dimension where many different spiral and even-odd states appear in the phase diagram, one can even detect the accurate phase boundary by the small anomaly in the magnetization curve, which was quite surprising to me.
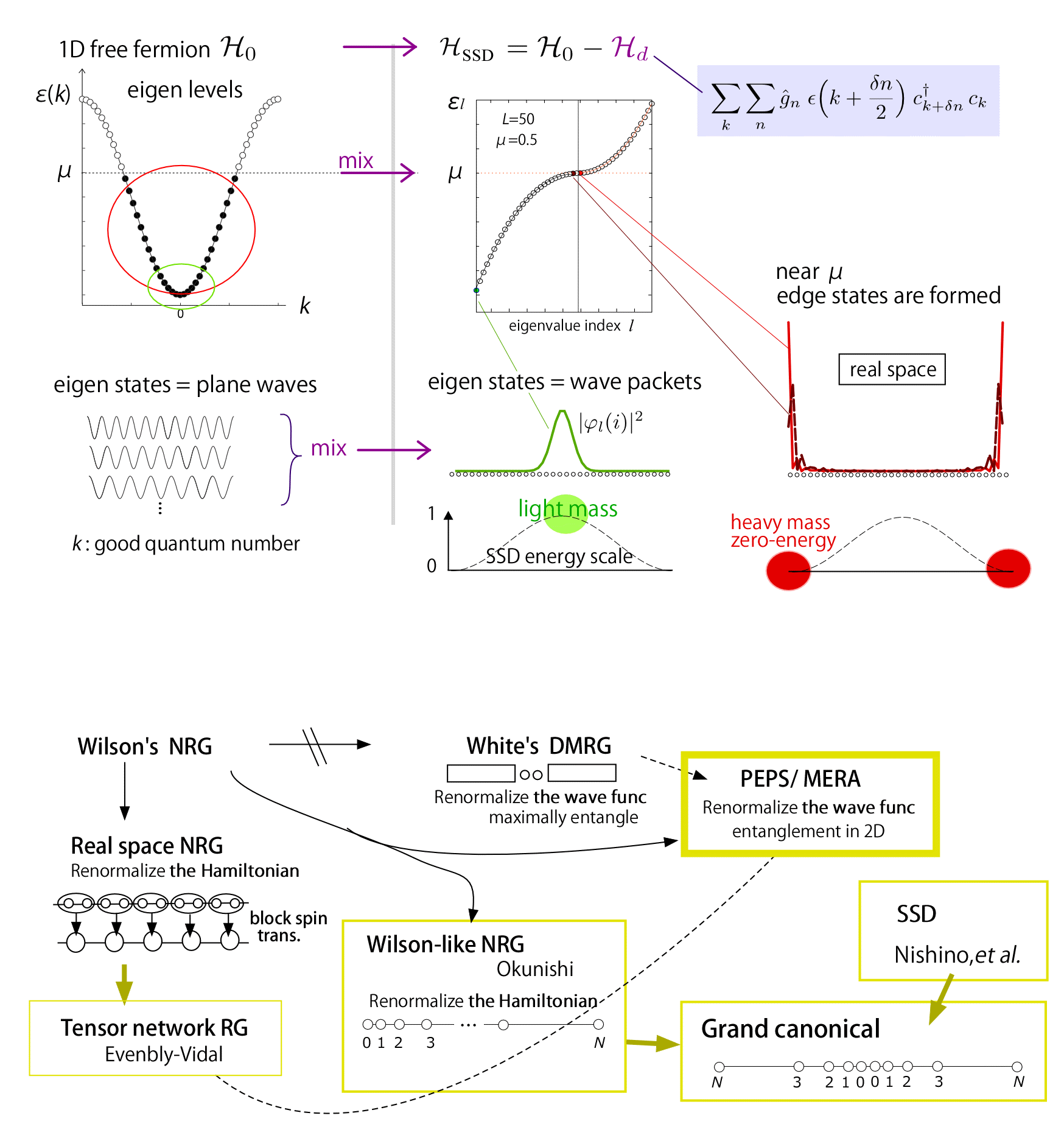
How does SSD work?
Q1:Can we adopt another functional form → NO. SSD is a magic function.
Q2:Which is better for 2D, Cartetian or polar?→ polar is better.
Placing SSD to the Hamiltonian means adding a scattering term. (Maruyama-Katsura-Hikihara2011). As a simplest example, let us consider a free fermionic cosine energy band. The energy eigen state at each k-point of the band is a plane wave. The scattering takes place between the two adjacent discrete energy levels in k-space. This is because the scattering wave number reflects the periodicity of the sine square function, charagerized by the single wavelength 2π/N, corresponding to the discreteness of k-space. As is well known, choosing a bunch of plane waves within the certain range of wave number, and taking linear combination, one can form a wave packet. The wave packet formed at the edge of the system has nearly zero energy, namely in the vicinity of μ. Whereas, those at the system center is formed at the bottom of the band. The edge states are densely distributed near μ (have a large density of states);. By using these edge states as baths, one can finely tune the number of particles at the system center.
Going back to Q1, if we use the functions other than SSD, the way the plane waves are mixed up becomes much more complicated, and the resultant distribution of states is not as ideal as the one we have for SSD.
Finite size effects
Let us briefly mention about the size effect.
(a) artificial discreteness of the wave number and the physical quantities accordingly,
(b) boundary effect
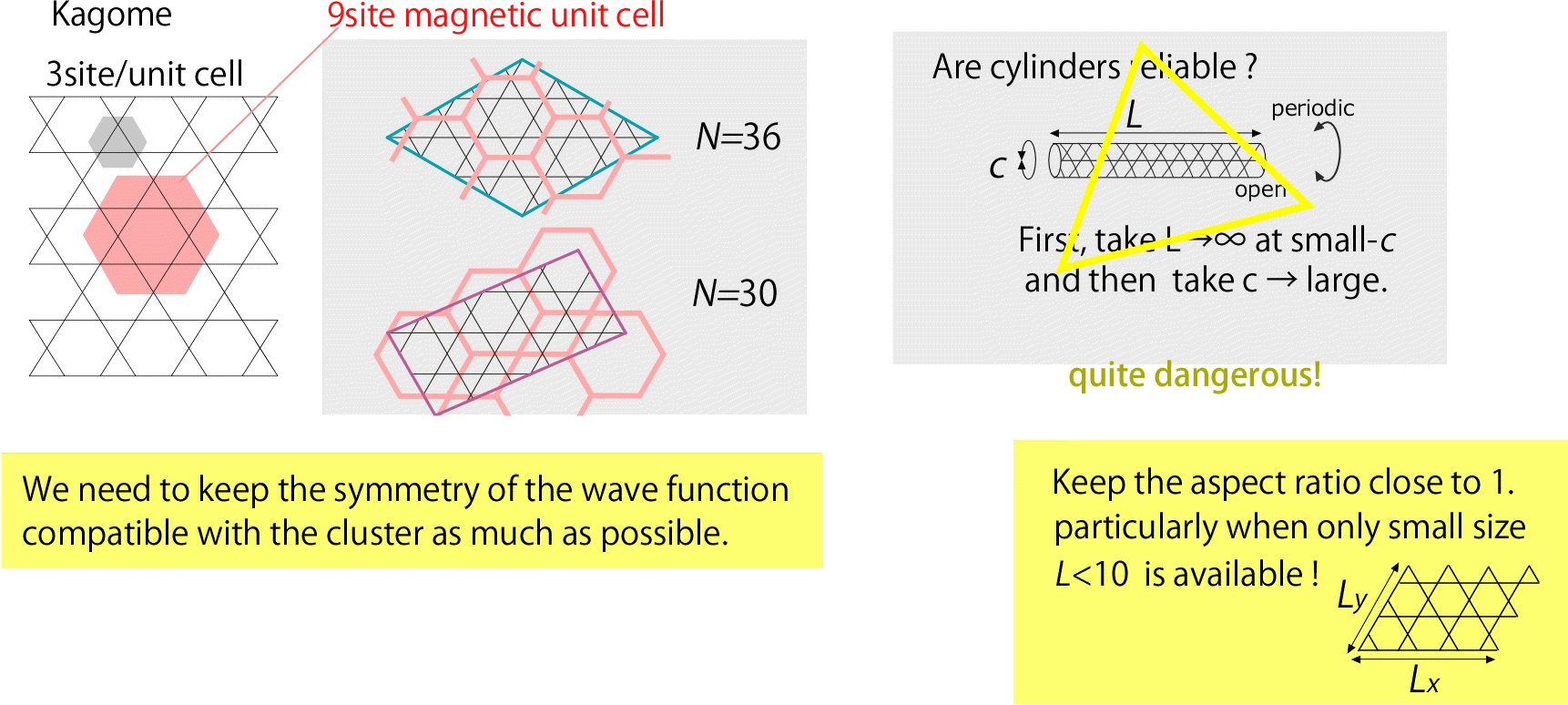
(c) cluster shapes/ aspect ratio
Here, (a) is the simplest and well known. The size scaling analysis often works well for 1D and 2D. However, there are some cases where the correlation develops in space, and when using DMRG with open boundary, the effect of Friedel oscillations cannot be easily get rid of. In the paper, [Shibata-Hotta, PRB 84 115116 (2011)] we have studied such difficult case and demonstrated how one can cope with such problem and examine very carefully the numerical results.
(c)aspect ratioF Recently, there are many works on cylinders, probably after the seminal work by Steve White's group on kagome. In fact it looks quite reasonable to apply a cylinderical geometry to DMRG because DMRG favors open boundary conditions. In these studies, usually the size along the radial direction is maximally about 10. The leg of the cylinder is first scaled toward ∞ for fixed radial size, and after that the size scaling in the radial direction is performed within a small size. However, it is quite probable that the size scaling by keeping the aspect ratio close to one gives different result from this kind of size scaling on cylinders. The danger of such analysis is pointed out in detail by Andreas Sandvik [PRB85, 134407(2012)]. We also showed for the kagome lattice antiferromagnet that the spin gap(at finite field) is significantly stabilized (artifactually) by the cylinder construction [Nishimoto-Shibata-Hotta, ncomm 4, 2287(2013)].
Let us briefly mention about the size effect.
(a) artificial discreteness of the wave number and the physical quantities accordingly,
(b) boundary effect
(c) cluster shapes/ aspect ratio
Here, (a) is the simplest and well known. The size scaling analysis often works well for 1D and 2D. However, there are some cases where the correlation develops in space, and when using DMRG with open boundary, the effect of Friedel oscillations cannot be easily get rid of. In the paper, [Shibata-Hotta, PRB 84 115116 (2011)] we have studied such difficult case and demonstrated how one can cope with such problem and examine very carefully the numerical results.
(c)aspect ratioF Recently, there are many works on cylinders, probably after the seminal work by Steve White's group on kagome. In fact it looks quite reasonable to apply a cylinderical geometry to DMRG because DMRG favors open boundary conditions. In these studies, usually the size along the radial direction is maximally about 10. The leg of the cylinder is first scaled toward ∞ for fixed radial size, and after that the size scaling in the radial direction is performed within a small size. However, it is quite probable that the size scaling by keeping the aspect ratio close to one gives different result from this kind of size scaling on cylinders. The danger of such analysis is pointed out in detail by Andreas Sandvik [PRB85, 134407(2012)]. We also showed for the kagome lattice antiferromagnet that the spin gap(at finite field) is significantly stabilized (artifactually) by the cylinder construction [Nishimoto-Shibata-Hotta, ncomm 4, 2287(2013)].