Numerical Methods
一般庶民でもきちんとした計算ができるようになる手法の会得や発展を目指しています. 決して世界であの人とあの人しかできないという計算ではありません. 我々の手持ちの手法としては exact diagonalization (ED), density matrix renormalization group (DMRG), classical Monte Carlo metrhod (MC), quantum Monte Carlo method(QMC)の一部 などですが, そのあたりの通常レベルの計算で物理の結論がクリアにつけられるような方法はないものかと普段から考えています. トピックスにもよりますが 理論屋として許されているカテゴリは主に3つあると思います,
(1) 物理的にきっちりとformulativeな解釈がつけられる問題+一体問題計算,
(2) 複雑な物質密着モデル+簡単な計算(平均場など)+意味のある物理描像,
(3) シンプルなモデル+ 量子多体計算
むろんこれらを組み合わせたり, この更に上を目指す方々もいらっしゃいます.
(3)はなかなかポンポン論文も出ず, 有意な結果を出すのが大変な しんどい世界です. その世界には, 数値計算にはプロならだれでも感じる「難しさ保存の法則」が存在します. 全く異なった方法論であるmodelの大変難しいparameter領域にapproach してみると結局似たり寄ったりの結果しか得られないのです. それでも挑みつづける少数の人々のストイックさを 日本の業界は, もっときちんと評価すべきだと常々考えています.
そこまで徹底したストイックさではないが(3)を志す我々が開発した/関わってきた手法を少しご紹介します.
Grand canonoical approach
[Hotta-Shibata PRB86 041108 (2012) , Hotta-Nishimoto-Shibata PRB 87115128 (2013) ]
「Hamiltonianは系の性質を決定するものであり, 気軽に変更するものではない, Hamiltonianを変更してしまうと物理が変わる」 これは物理屋の誰もがもつ固定観念であり, 正しいstatementでもあります. これに対して, 「系の実空間-虚時間空間が虚時間方向に”曲がっているとき", 波動関数を不変に保つために, Hamiltonianを空間変調してしてしまおう」という一見突拍子もないことを2010年ごろ考えたのが Nishinoさんです. その後 この考え方は様々な形で発展し, 現在ではsine square deformation (SSD)と呼ばれるHamiltonianの変換をすることが 比較的広い範囲で受け入れられるようになりました. このSSDがまだ海のものとも山のものともわからない(失礼!)時期に これを数値計算に利用し, 有限サイズ効果(注)を消去する ことができたのが 我々の grand canonical analysis です.
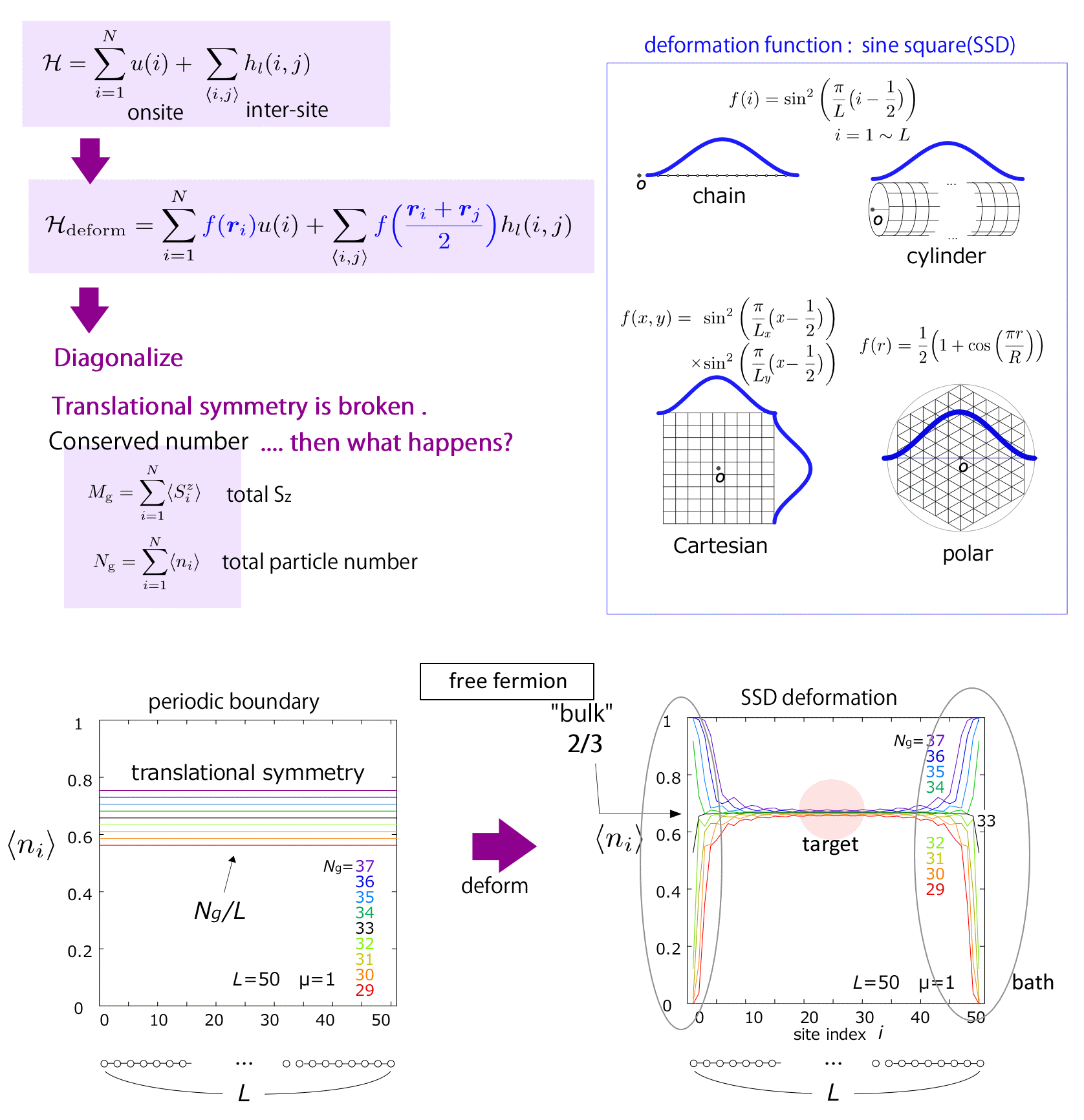
元々有限サイズでperiodic boundary条件(PBC)のもとでの量子計算では系の並進対称性を反映し, あらゆる物理量が一様な値を取ります. Hamiltonianには保存量があります. 例えば粒子数Ngや磁化Mgなどです. これに対応したサイトごとの粒子密度や磁化密度は Ng/N, Mg/Nの値で一定となります (Nはシステムサイズ). 手でグランドポテンシャル項をHamiltonianに加え, 化学ポテンシャルμ (磁化に対しては磁場 h) を変えてもその結果には何ら影響しません. (ちなみに開放系でμを与えるとμに対応した粒子数が得られるが, 有限孤立系の計算では粒子数Ngを手で与えねばならない).
そこへ HamiltonianにSSD変換をかけます. すると 並進対称性が失われ, 波動関数が変形します. SSDは系の端でゼロ, 中央で1となるような envelope関数であり, Hamiltonianのエネルギースケールを 空間変調させます.
図は1次元free fermion系でように並進対称であった粒子数の期待値が, SSD変換後にどう変調するかを示したものです. 手で与えた化学ポテンシャル μ を一定に保ち, 系の全粒子数 Ngを変えていくと, 実空間の粒子数分布が組み変わります. 系の端の粒子数は激しく変動するのに対して, 中央は μ に本来 N=∞ で対応すべき粒子数に相当する値付近で ほぼ一定にとどまっています. この中央での値を取り出すことにより 実際に1次元系では10-4程度の精度で N=∞ における物理量の値と 遜色ない物理量をわずかN=10-50程度の系で得ることができます. ここでおこっていることは, 系の端を緩やかな粒子浴として, 系の中央の粒子数が足りなければ端から引っこ抜いて補充し, 多すぎれば端に押しやるという不思議な挙動です.
例えばDMRGの計算を行う際, 複数のサイズ, N=50,100, 150, ...を計算し, 物理量を 1/Nでプロットし N=∞ に外挿するという方法が一般的です. しかしこのスケーリングは系の相関長が長くなるとあまりきれいにいかなくなるなど 極度に難しいパラメタ領域では 困難が生じることも過去に近藤格子系の研究を行っていた際に経験していました.
また例えば系が並進対称性を破って特殊な秩序を作っているときm倍周期の状態をうまく記述するには Nがmの倍数で なければならず incommensurate (長い周期, 例えばスパイラル)な変動する周期の物理状態に対しては あまり質の良い計算ができず有意な結論を得るにはかなりの努力が要求されていました. grand canonical methodを用いることによりこの問題は解消されます. 実際に 1次元でスパイラルやeven odd相が出るJ1J2modelについての結果を 最初の論文に載せましたが, この系の複雑な相境界までが磁化過程からdetectできることに 計算をしていて実際 驚きました.
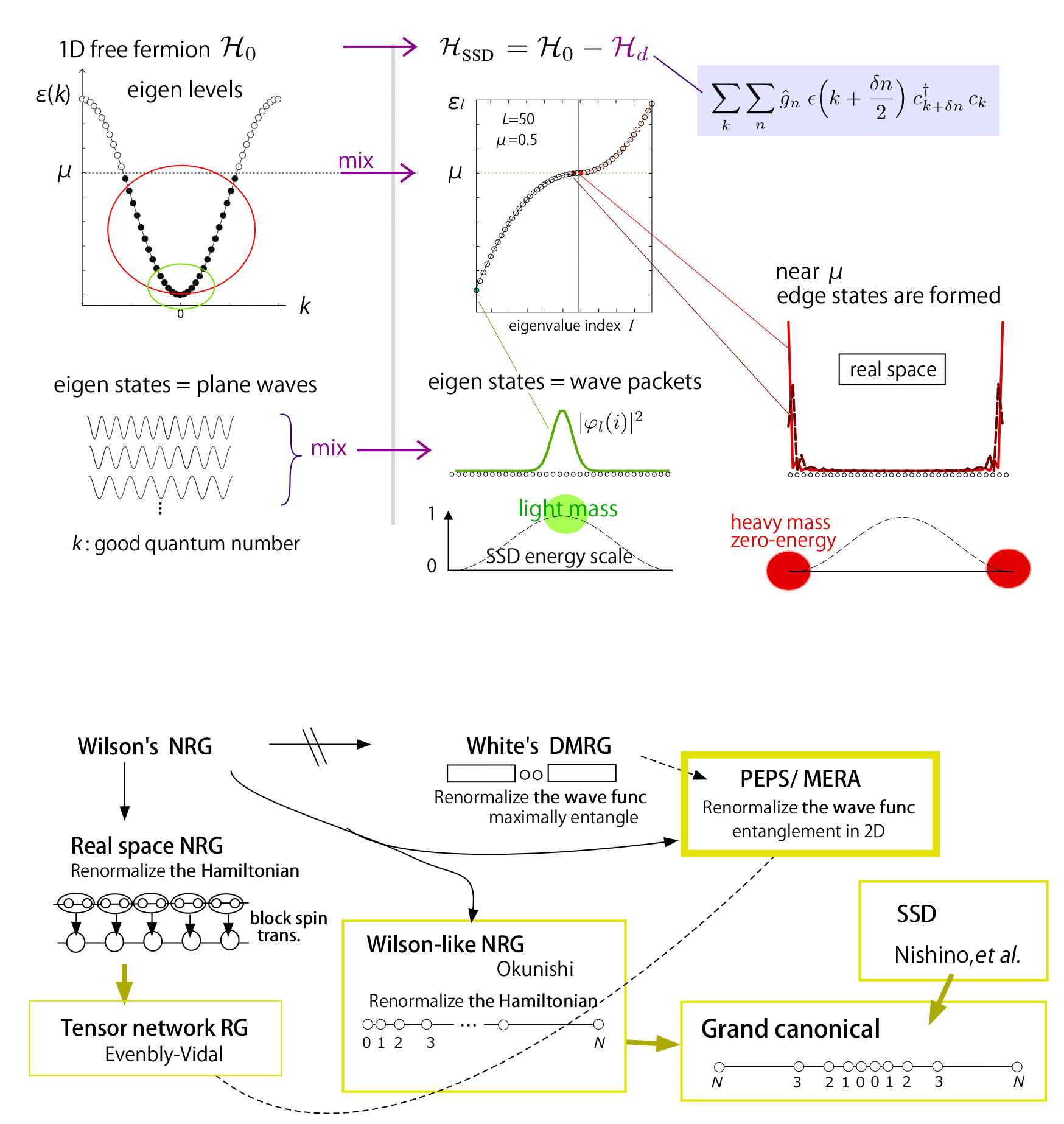
SSDは何をしているのか?
Q1:他の関数ではだめなのか?→ ダメです. SSDは magic functionです.
Q2:2次元だと Cartetianと polarとどちらが良いのか?→ ダメです. polarです.
元の一様なHamiltonianに対してSSDを加えることは, ある散乱項を加えることに相当します (Maruyama-Katsura-Hikihara2011). たとえばfree fermionのバンドを考えましょう. 波数kの関数としてcosの形をとっており, バンドの各固有状態は平面波です. そこに導入された散乱項は, SSD関数が系全体にわたる長波長の逆数(2π/N)に相当する小さな一つの波数だけで 特徴づけられることを反映し, 波数空間でその波数(2π/N)だけ異なった状態同士を混ぜ合わせます.
よく知られているようにある一定のレンジの波数の平面波を重ね合わせると波束ができます. そのレンジが広いほど波束は鋭く局在します. SSDによる混成の強度はエネルギーがμ から離れれば離れるほど大きくなるようにできているので μに近い状態ほど緩やかにたくさんの波につながった混成が起き, 広いレンジの波数を拾って 局在した波束を形成するのです. ここでμに近い状態の波束はもともとエネルギーがゼロに近いという意味で系のエッジに分布します. この鋭い波束の状態の状態密度は大きく, かつ系の中央への波動関数のテールは非常に小さいことから μ付近の状態が端にたまってgrand canonical粒子浴として機能し, システムの中央での粒子の分布を うまくコントロールできる仕組みになっています. 少し見方を変えると, 系の端では実効的にゼロエネルギー, 中央ではもとのエネルギースケールを反映した 物理が実現する, それぞれの領域に局在する波束はそれぞれのエネルギースケールの状態を代表している, ともいえます.
Q1にもどると, SSD以外の関数を使った場合, 多くの波数の平面波同士の混成が起こってしまいあまりきれいな波束が作れなくなってしまいます. またQ2の2次元ではpolarがよいということは経験則ではわかっていたのですが, 最近 Katsuraらが球系の解析計算をして傍証的に理解を深めています.
図のWilson's NRGのchartについて: 私見ですが 最近のいろいろな数値計算(周辺の人々の仕事)を見ていて だいたいこんな流れの中でgrand canonicalは理解できるのかなと考えています. ここにあげているいくつかの手法に関連した話題は 機械学習の発展と相まって これからまたどんどん理解が発展していくと思います.
(episode) 大学院生さんたちにはぜひそういう経験をしてほしいと思うので少し書いてみました: grand canoは 2011年 仙台駅の郵便局のベンチで自転車を繰り出して山を下りてきたShibataさんと 彼のとある計算結果を見て議論をしていた ある瞬間, まさに電球が頭にぽっと浮かぶような感じで思いついた. これはいける と思い, 京都に帰った足から 大量に1d スピン系のDMRG計算を走らせ, データをとりまくって整理してまとめて論文にしたことを覚えている. 当時はただの思い付き+経験則だった. その後 Maruyamaらや Okunishi-Nishinoの論文 をパラパラ読みながらなんとなしに考えていて, なんだもしかしてこれは波束化か と思い, ふたたび狂ったようにfree fermion の計算(一瞬で終わる)をして, 実空間繰り込み的な理解を獲得した. このころたまたま京大で振動波動論の講義をしていたことに心から感謝した. 講義は研究の役に立ちます.
今では SSD fan club memberもふえ, マニアックながらそれなりの理解の発展をしていると思う.
有限サイズ効果
世間では非常によく知られている言葉ですが 世の中が意外に鈍感な気がするので(鈍感が必要な場合もありますが) 以下気になることを書いておきたいと思います. 有限サイズ効果には主に3種類あります.
(a) 得られる状態の波数/物理量のサイズNに応じたartificialな離散性,
(b) boundary効果
(c) 有限サイズクラスタ効果 / aspect ratio問題
このうち(a)は単純に学部生の量子力学の問題で 波数がシステムサイズNに応じて2π/N x 整数に離散化されるというものです. サイズが小さいと許されるエネルギーレベルが離散的なのでそれに応じて物理量も離散的に見えますが サイズが大きくなると最終的には連続的な関数に外挿します. 固体物性は無限系(bulk)でwell definedな熱力学量を観測し, 理解する学問なので 離散的なのは困るのです. 低次元系の場合はscaling 関数の素性が知られていて 1/N →0に向けて物理量の外挿がうまくいくことも多いです. また有限温度の2次転移を議論する場合は finite size scaling analysisがしばしば適用されます: これは転移点近傍で scale freeな関数が存在すると仮定し, 小さなサイズの計算でもあるルールでスケール変換を行うことで サイズに依存しないuniqueな曲線に計算量が載るというものです. 臨界指数を解析したり 相転移の存在を示したりすることに利用されています.
(b)については 一般にopen boundaryの場合には 開いた端が系に対して impurityのようにふるまい Friedel振動が起こるという 効果に関するものです. 本来この振動は 1/L (:Lは端からの距離)以下で減衰してしかるべきですが 相関距離が非常に長い難しい状態を数値計算で扱う場合には この境界効果が大きすぎて(a)のサイズ効果と相乗の負の効果を およぼし, 正しい結論を得ることが困難になることがあります. これに関しては [Shibata-Hotta, PRB 84 115116 (2011)] という7年ごしの コスパの悪さにかけては最高レベルに近い仕事もあるのでご参照いただきたい. 当時我々にとってはとても大事な問題だった件をものすごくしつこく調べたものです.
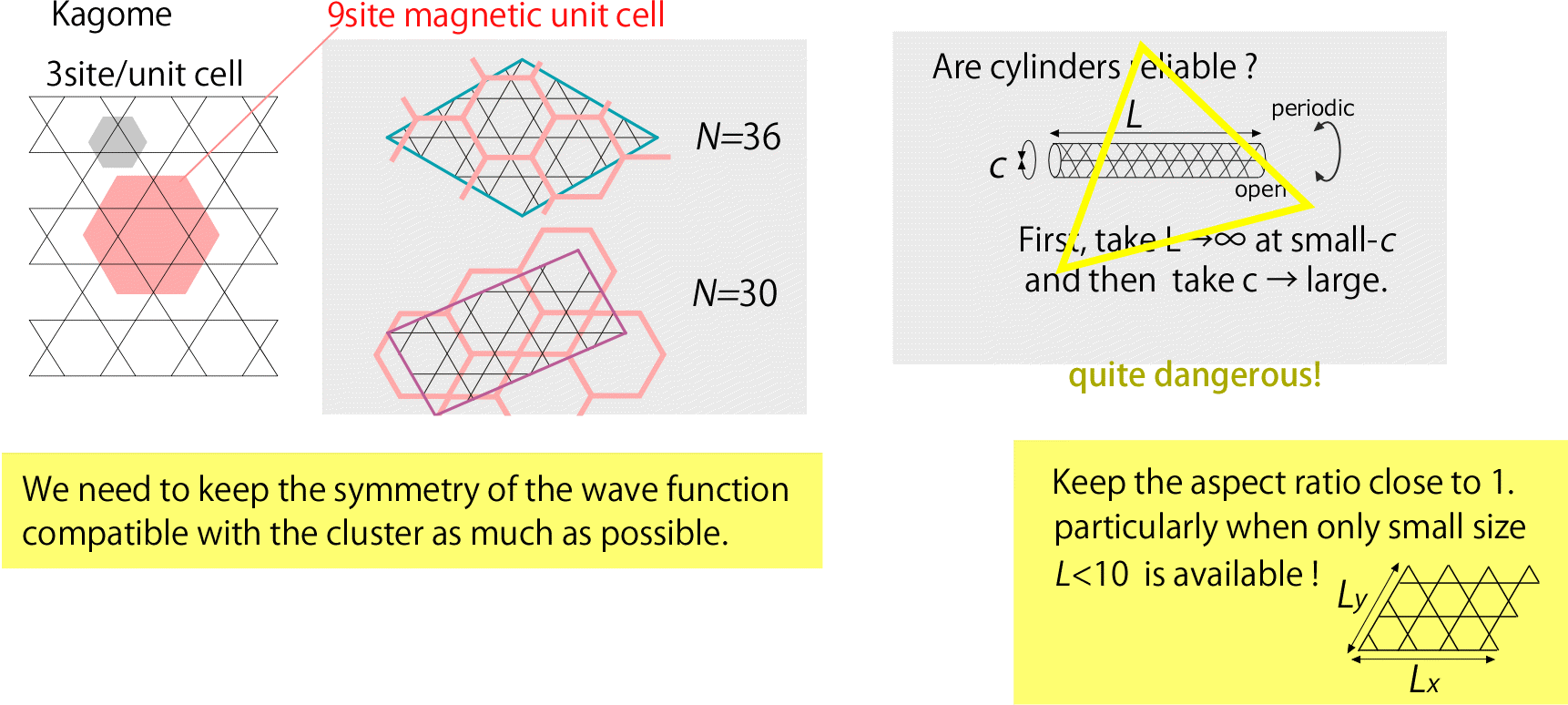
(c)に関して:もともと結晶をモデル化した系はunit cellを単位に並進対称性を持ちます. 量子計算の場合, 前述のようにあらゆる物理量は periodic/antiperiodicな境界条件をかけた場合, つねに並進対称です. ただしときに系が非常に強い相関を発達させたり 相転移によりunit cellの周期が大きくなる場合があります. その際 有限サイズクラスタの計算において新しいunit cellに整合するような格子構造を持っていない場合は 状態をunitでつなぎ合わせて格子を作成したとき必ずどこかに不具合が起こります, それを解消するために artificialにエネルギーがあがってしまいます. 我々の目的の多くは「最もエネルギーが安定な状態」=基底状態 およびそれと競合する低エネルギー状態の 波動関数を絶対零度で正しく求めることですがこの不具合によってエネルギーの利得が変わってしまうと当然正しい 結果が得られません.
例えばKagome磁性体においては 絶対零度で期待されているスピン液体の対抗馬として valence bond crystal状態と呼ばれる unit cellが36サイトにもわたる 状態が安定なのではないか?という議論があります. しかしほとんどの計算はこの36サイトにわたる計算をまともに 精度よく行うことがむつかしく有意な比較をすることは困難です(この効果以外に近似の方法の特性の問題もあるので単純ではない).
次いで aspect ratioの問題に言及したいと思います. kagomeの話題にも関連しますが, できるだけ大きな系で計算を行おうと, 各所でcylinder DMRGという方法が今全盛を迎えています. DMRGはもともとopen boundaryをもつことによって精度を上げる方法なので2次元系を計算する際にある方向をperiodic, 別の方向をopenにすることは理にはかなっています. 実際, cylinderの計算によっていろいろfancyな物理を提示されているのですが, 少し注意が必要です. 一般に計算が可能なcylinderの周長がおよそmax10くらいです. そこで周長を6,8,10などと設定したものそれぞれに対してcylinderのlegを無限大まで伸ばした場合の物理量を求め, さらに小さな周長に関してサイズスケールしていくわけです. しかし本当はaspect ratioを保ったLxLでじわじわとLを変えない限り正しいスケーリングができないことが 非常に多いということは知る人は良く知っています. この点で QMC業界の鉄人, Andreas Sandvik の論文[PRB85, 134407(2012)] は非常に教育的です. [Nishimoto-Shibata-Hotta, ncomm 4, 2287(2013)] の supplementaryにもいかにcylinderがまずいかということを示してあります. 「Cylinders are cylinders, not the BULK.」といいたいところですが, 一方で そこに物理があるのにやれる計算をやりたいという気持ちも わからなくもないのであれもダメこれもダメと言ってしまっても...というところがつらいところです.
世間では非常によく知られている言葉ですが 世の中が意外に鈍感な気がするので(鈍感が必要な場合もありますが) 以下気になることを書いておきたいと思います. 有限サイズ効果には主に3種類あります.
(a) 得られる状態の波数/物理量のサイズNに応じたartificialな離散性,
(b) boundary効果
(c) 有限サイズクラスタ効果 / aspect ratio問題
このうち(a)は単純に学部生の量子力学の問題で 波数がシステムサイズNに応じて2π/N x 整数に離散化されるというものです. サイズが小さいと許されるエネルギーレベルが離散的なのでそれに応じて物理量も離散的に見えますが サイズが大きくなると最終的には連続的な関数に外挿します. 固体物性は無限系(bulk)でwell definedな熱力学量を観測し, 理解する学問なので 離散的なのは困るのです. 低次元系の場合はscaling 関数の素性が知られていて 1/N →0に向けて物理量の外挿がうまくいくことも多いです. また有限温度の2次転移を議論する場合は finite size scaling analysisがしばしば適用されます: これは転移点近傍で scale freeな関数が存在すると仮定し, 小さなサイズの計算でもあるルールでスケール変換を行うことで サイズに依存しないuniqueな曲線に計算量が載るというものです. 臨界指数を解析したり 相転移の存在を示したりすることに利用されています.
(b)については 一般にopen boundaryの場合には 開いた端が系に対して impurityのようにふるまい Friedel振動が起こるという 効果に関するものです. 本来この振動は 1/L (:Lは端からの距離)以下で減衰してしかるべきですが 相関距離が非常に長い難しい状態を数値計算で扱う場合には この境界効果が大きすぎて(a)のサイズ効果と相乗の負の効果を およぼし, 正しい結論を得ることが困難になることがあります. これに関しては [Shibata-Hotta, PRB 84 115116 (2011)] という7年ごしの コスパの悪さにかけては最高レベルに近い仕事もあるのでご参照いただきたい. 当時我々にとってはとても大事な問題だった件をものすごくしつこく調べたものです.
(c)に関して:もともと結晶をモデル化した系はunit cellを単位に並進対称性を持ちます. 量子計算の場合, 前述のようにあらゆる物理量は periodic/antiperiodicな境界条件をかけた場合, つねに並進対称です. ただしときに系が非常に強い相関を発達させたり 相転移によりunit cellの周期が大きくなる場合があります. その際 有限サイズクラスタの計算において新しいunit cellに整合するような格子構造を持っていない場合は 状態をunitでつなぎ合わせて格子を作成したとき必ずどこかに不具合が起こります, それを解消するために artificialにエネルギーがあがってしまいます. 我々の目的の多くは「最もエネルギーが安定な状態」=基底状態 およびそれと競合する低エネルギー状態の 波動関数を絶対零度で正しく求めることですがこの不具合によってエネルギーの利得が変わってしまうと当然正しい 結果が得られません.
例えばKagome磁性体においては 絶対零度で期待されているスピン液体の対抗馬として valence bond crystal状態と呼ばれる unit cellが36サイトにもわたる 状態が安定なのではないか?という議論があります. しかしほとんどの計算はこの36サイトにわたる計算をまともに 精度よく行うことがむつかしく有意な比較をすることは困難です(この効果以外に近似の方法の特性の問題もあるので単純ではない).
次いで aspect ratioの問題に言及したいと思います. kagomeの話題にも関連しますが, できるだけ大きな系で計算を行おうと, 各所でcylinder DMRGという方法が今全盛を迎えています. DMRGはもともとopen boundaryをもつことによって精度を上げる方法なので2次元系を計算する際にある方向をperiodic, 別の方向をopenにすることは理にはかなっています. 実際, cylinderの計算によっていろいろfancyな物理を提示されているのですが, 少し注意が必要です. 一般に計算が可能なcylinderの周長がおよそmax10くらいです. そこで周長を6,8,10などと設定したものそれぞれに対してcylinderのlegを無限大まで伸ばした場合の物理量を求め, さらに小さな周長に関してサイズスケールしていくわけです. しかし本当はaspect ratioを保ったLxLでじわじわとLを変えない限り正しいスケーリングができないことが 非常に多いということは知る人は良く知っています. この点で QMC業界の鉄人, Andreas Sandvik の論文[PRB85, 134407(2012)] は非常に教育的です. [Nishimoto-Shibata-Hotta, ncomm 4, 2287(2013)] の supplementaryにもいかにcylinderがまずいかということを示してあります. 「Cylinders are cylinders, not the BULK.」といいたいところですが, 一方で そこに物理があるのにやれる計算をやりたいという気持ちも わからなくもないのであれもダメこれもダメと言ってしまっても...というところがつらいところです.