Frustrated magnetism
Here we introduce some of our works on kagome lattice.
Kagome lattice magnets
Spin gaps in the ground state
The ground state of the S=1/2 kagome lattice antiferromagnet is considered to be a possible spin liquid. [see Han et al, 2012, Mendels, 2007 for experiments] In theories, [ for early studies Poilblanc, Misguish, Read-Sachdev, etc.], there are several measure for spin liquids. One is the topological term in the entanglement entropy, which is actually calculated for kagome lattice and its analogues by Jiang et al. and Depenbrock et al. in 2012. However, notice that this quantity has a nonnegligible size effect. There are other ways, such as examining the topological degeneracy by making use of the cylinder construction, or by plotting the entanglement spctrum [for chiral spin liquid in decorated kagome, Gong-Zhu-Sheng 2014].
There is a long discussion on whether the ground state of the kagome lattice antiferromagnet is spin gapped or not, and if yes, how large it should be. The old ED paper by Waldtmann, et al.1998 gives the size of the gap~J/20 based on the even and odd size scaling. The DMRG calculation keeping the aspect ratio to 1 is made by Jiang-Weng-Sheng 2008 which also gives J/20. The papers by Yan-Huse-White, Depenbrock-McCulloch-Schollwock [cylinder DMRG] concludes from their analysis that the value is at around J/10. He-Zaletel-Oshikawa-Pollmann[cylinder DMRG + boundary shift] says that it is gapless (Dirac). In our paper [Nishimoto-Shibata-Hotta 2013] we consider that the cylinderical construction overestimates the gap (it is actually demonstrated in the supplementary) and we expect the gap to be as small as J/20 (or smaller) by the small step in the magnetization curve at around zero field.
Recently, by evaluating the finite temperature susceptibility [Hotta-Asano, PRB 98 140405(R) (2018)] we see that the gap can be even smaller. Tao Xiang (tensor) and Frederico BeccaiVMC) 's works consider the system to be gapless. I guess the issue is not settled, maybe never!
Magnetization curve of kagome
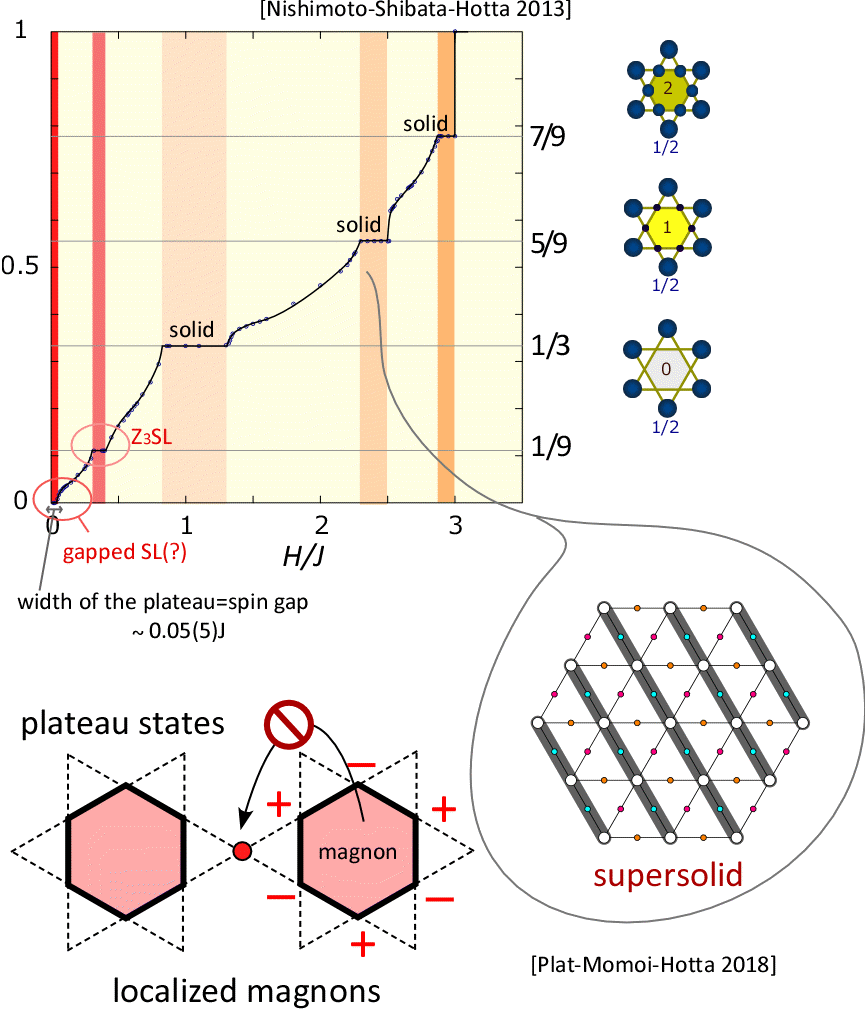
In [Nishimoto-Shibata-Hotta Nature Comm. 42287, 2013] the magnetization curve of the kagome antiferromagnet is obtained based on the grand canonical analysis applied to DMRG. Five plateaus including the ground state one is found (1/3, 7/9 are already known). 1/3, 5/9, 7/9 plateaus are the magnon solids with extended unit cell consisting of 9 sites in the shape of the star of David. The edges of the stars have spin-up, and the central hexagon of the star accomodate 1/2/3 magnons fpr 1/3, 5/9, 7/9 plateaus, respectively. In the 1/9 plateau we could not find any sign of symmetry breaking, and the topological term of the entanglement entropy gave -ln 3, indicating that this is a spin liquid plateau.
The phase just below the 5/9 plateau can be a supersolid [Plat-Momoi-Hotta PRB 98, 014415 (2018)]. This work sheds light on the different aspect of kagome, which is the kinetic frustration effect. Let us consider a 5/9 plateau phase: when these magnons try to hop outside this hexagon, there are two hopping contributions from the adjacent hexagonal sites to the edge of the star with the same amplitude and with different signs, which cancel with each other. This kind of destructive interference, which is the kinetic frustration effect, is well known for the origin of the flat band ferromagnetism as well as the magnetization plateau phases of the Shastley-Sutherland model. Similar distructive interference occurs for higher excited states of the plateau. Since some of the hopping contributions remain finite including those of the higher order hopping that transfers the magnon to further distance, the resultant hopping paths become extremely complicated. In such case, more than two hopping processes often interfere, and makes the bandwidth of the excited magnons narrow. When the magnon branch goes down with varying the field and finally reaches the energy level of the plateau, the instability to another phase takes place. For the lower-field instability of the 5/9 plateau phase, the emergent phase is the supersolid phase, where the interplay of repulsive interaction and the kinetic frustration is crucial.
Excitation spectrum
We have recently developed a numerical method to exactly obtain the response functions against the weak to strong external field, [χ(q,ω)]. [Endoh-Hotta-Shimizu PRL121 220601 (2018)]. The advantage of this method is that the result is numerically almost exact for that system size: it reproduces well the linear response functions for small field, while can be applied to cases with any field strength.
By applying this method to the kagome lattice antiferromagnet, we obtained an excitation spectrum [Im chi(q,omega)] in both the linear and nonlinear response regimes. The exotic features of the kagome lattice is observed: There is a broad peak at low energy part of the spectrum whose shape does not show any significant k(wave number)-dependence. This may indicate that there is a spinon excitation from the ground state, and it does not depend on k (nearly localized?).
Kagome electrons
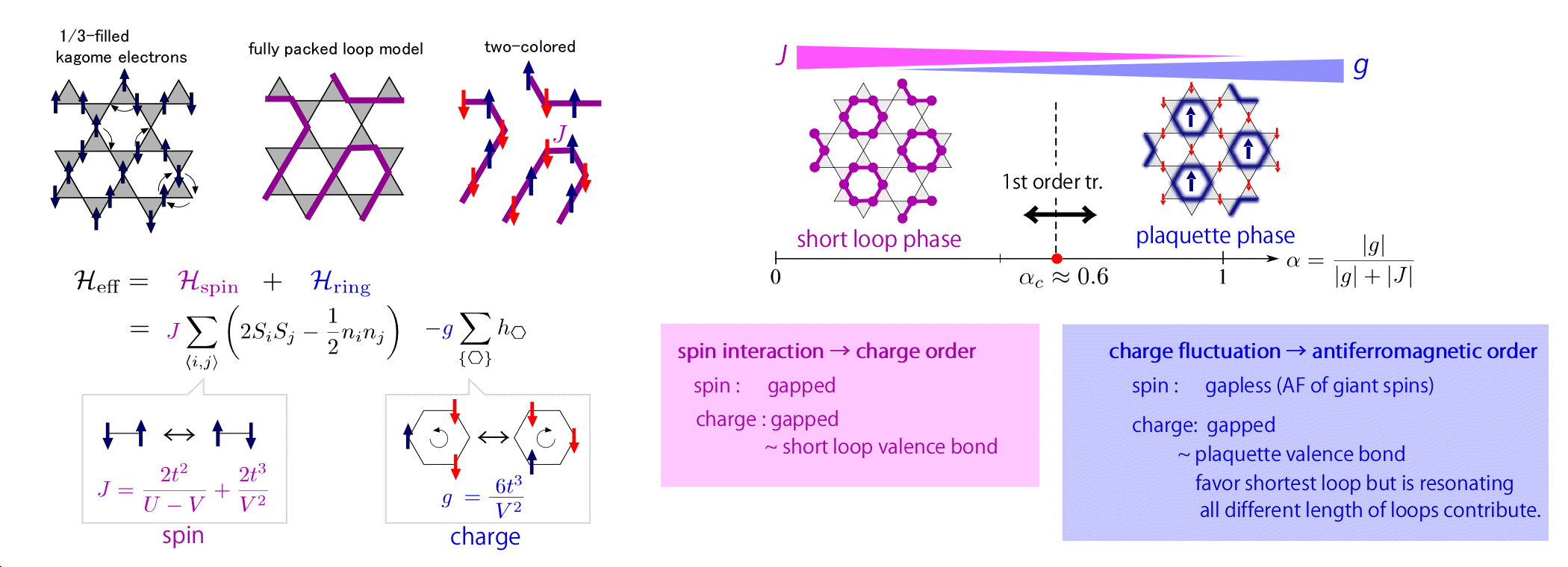
This is the old work [Pollmann-Roychowdhury-Hotta-Penc, PRB 90 035118 (2014)]. There we considered a strongly interacting electronic systems with a filling factor of 1/3. In order to favor the neighboring repulsive interaction V and on-site U in the strong coupling regime, the electrons distribute in a way to fill two sites without double occupancy in each triangular unit. There are numerous numbers of degenerate manifolds of states that fulfills this charge distribution, and by considering the spin degrees of freedom, the degeneracy is multiplied. The question was how this degeneracy is lifted by the fluctuation of spins and charges. The dynamics of charges can be cartooned by the so-called fully packed loop model (it is a loop model on a dual honeycomb lattice but here it is easier to write it down on the kagome lattice). One can form a closed loop by connecting the neighboring charges, and the fluctuation of charges represented by g reorganizes the loop configuration. On the other hand, the spins living on loops interact antiferromagnetically by J with its neighbors. Therefore, there is a contribution from this magnetic part to stabilize certain types of loops. This kind of competition/interplay of J and g gives rise to the picture that the spin interactions will stabilize the charge order, and the charge fluctuation will stabilize the magnetic ordering. The resultant phase itself looks not at all exotic, but there is some nontrivial underlying physics behind.
In [Nishimoto-Shibata-Hotta Nature Comm. 42287, 2013] the magnetization curve of the kagome antiferromagnet is obtained based on the grand canonical analysis applied to DMRG. Five plateaus including the ground state one is found (1/3, 7/9 are already known). 1/3, 5/9, 7/9 plateaus are the magnon solids with extended unit cell consisting of 9 sites in the shape of the star of David. The edges of the stars have spin-up, and the central hexagon of the star accomodate 1/2/3 magnons fpr 1/3, 5/9, 7/9 plateaus, respectively. In the 1/9 plateau we could not find any sign of symmetry breaking, and the topological term of the entanglement entropy gave -ln 3, indicating that this is a spin liquid plateau.
The phase just below the 5/9 plateau can be a supersolid [Plat-Momoi-Hotta PRB 98, 014415 (2018)]. This work sheds light on the different aspect of kagome, which is the kinetic frustration effect. Let us consider a 5/9 plateau phase: when these magnons try to hop outside this hexagon, there are two hopping contributions from the adjacent hexagonal sites to the edge of the star with the same amplitude and with different signs, which cancel with each other. This kind of destructive interference, which is the kinetic frustration effect, is well known for the origin of the flat band ferromagnetism as well as the magnetization plateau phases of the Shastley-Sutherland model. Similar distructive interference occurs for higher excited states of the plateau. Since some of the hopping contributions remain finite including those of the higher order hopping that transfers the magnon to further distance, the resultant hopping paths become extremely complicated. In such case, more than two hopping processes often interfere, and makes the bandwidth of the excited magnons narrow. When the magnon branch goes down with varying the field and finally reaches the energy level of the plateau, the instability to another phase takes place. For the lower-field instability of the 5/9 plateau phase, the emergent phase is the supersolid phase, where the interplay of repulsive interaction and the kinetic frustration is crucial.
Excitation spectrum
We have recently developed a numerical method to exactly obtain the response functions against the weak to strong external field, [χ(q,ω)]. [Endoh-Hotta-Shimizu PRL121 220601 (2018)]. The advantage of this method is that the result is numerically almost exact for that system size: it reproduces well the linear response functions for small field, while can be applied to cases with any field strength.
By applying this method to the kagome lattice antiferromagnet, we obtained an excitation spectrum [Im chi(q,omega)] in both the linear and nonlinear response regimes. The exotic features of the kagome lattice is observed: There is a broad peak at low energy part of the spectrum whose shape does not show any significant k(wave number)-dependence. This may indicate that there is a spinon excitation from the ground state, and it does not depend on k (nearly localized?).
Kagome electrons
This is the old work [Pollmann-Roychowdhury-Hotta-Penc, PRB 90 035118 (2014)]. There we considered a strongly interacting electronic systems with a filling factor of 1/3. In order to favor the neighboring repulsive interaction V and on-site U in the strong coupling regime, the electrons distribute in a way to fill two sites without double occupancy in each triangular unit. There are numerous numbers of degenerate manifolds of states that fulfills this charge distribution, and by considering the spin degrees of freedom, the degeneracy is multiplied. The question was how this degeneracy is lifted by the fluctuation of spins and charges. The dynamics of charges can be cartooned by the so-called fully packed loop model (it is a loop model on a dual honeycomb lattice but here it is easier to write it down on the kagome lattice). One can form a closed loop by connecting the neighboring charges, and the fluctuation of charges represented by g reorganizes the loop configuration. On the other hand, the spins living on loops interact antiferromagnetically by J with its neighbors. Therefore, there is a contribution from this magnetic part to stabilize certain types of loops. This kind of competition/interplay of J and g gives rise to the picture that the spin interactions will stabilize the charge order, and the charge fluctuation will stabilize the magnetic ordering. The resultant phase itself looks not at all exotic, but there is some nontrivial underlying physics behind.