Frustrated systems
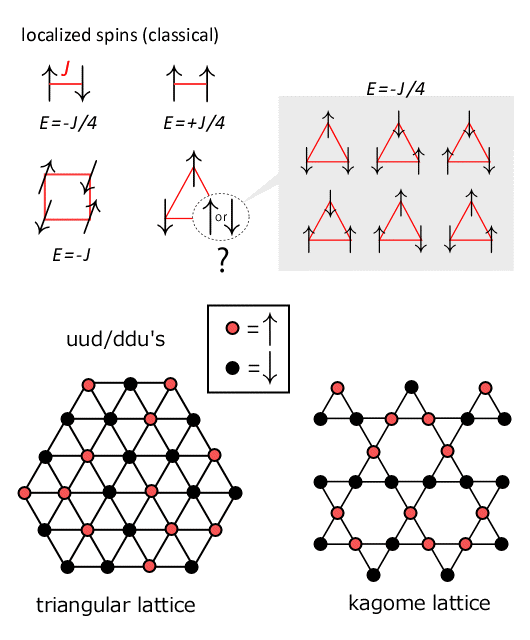
フラストレーションという言葉は 1970年代スピングラスの研究 で Andersonが導入したもので, ローカルな相互作用エネルギーの利得を全部満たそうとしてもうまくいかないこと, つまり一つ一つの相互作用が最も低くなるようなスピン配置を全系にわたって作ろうとすると不具合が生じて かなりの割合で相互作用が損をしてしまう状況をいいます. スピングラスの場合はランダムに +/-で分布した磁気的相互作用のことを意味しています. 似たような状況を一様な結晶系で実現するためには 幾何学的フラストレーションか長距離相互作用が必要となります. フラストレーションがある格子の代表例は三角と籠目です.
三角も籠目も 三角形をunitにしており antiferro的な相互作用(spinが反対向きにそろった方がエネルギーが得) のもとで このunit上で最低エネルギーとなるパターンが6種類あります(uud or ddu). この三角を edge/corner sharingでつなぎ合わせると三角/籠目格子ができます. その際 すべての三角unitをuud/ddu にしようとすると古典的には Hilbert空間の次元の半分程度にわたる縮退を持った 基底状態となります(熱力学第三法則の破れ). このように低エネルギー状態の縮退度が高いほどフラストレーションの度合いが大きいと理解されており, フラストレーションを定量化するためのmeasureもいくつか提案されています.
上述のunusualな縮退は偶然縮退であり 摂動に弱いという性質があります. そのため量子揺らぎや温度揺らぎが主役となって新しい相ができます (order by disorder).
籠目格子の磁性, 電子系について以下簡単にご紹介します. こちらはやや専門家向けの解説(私説, 概観)であり, 古い研究ほど情報が少なめになっています. 三角格子の電子系などについては organicsをご覧ください.
Kagome lattice magnets
基底状態の spin gap 問題
S=1/2の籠目格子Heisenberg modelの基底状態はスピン液体だと言われています. 仕事はほぼ無数にありますが [Hanら2012, Mendels2007] などが実験ではよく知られています. 理論では初期には[Poilblancら, Read-Sachdev] など. スピン液体かどうかに関しては 現在いくつか判断する指標があります. ひとつは Jiangら や Depenbrockらによって籠目に適用された(2012) entanglement entropyのtopological項の解析です. ただしこの量にはかなり大きな有限サイズ効果があるのでトップデータだけを出しているかもしれない論文にはやや 注意が必要な場合がありますし, spin gapのある系でしか利用できません. (topological 縮退も同様です). 一時期, すべてのgapped spin liquidがZ2になってしまうのはなぜだろう問題が (ヨーロッパ量子スピンマニアの集団で)議論になりました. ほかにentanglement spectrumもdecorated kagomeのchiral spin liquidの同定に使われています[Gong-Zhu-Sheng 2014].
S=1/2 kagomeの基底状態に spin gapがあるか否か, に関しては長いこと議論がされています. 非常に古いEDではWaldtmann, et al.1998が J/20を出しています(直感的?さすがEDのプロ集団です). これまでの数値計算として有意なものに Jiang-Weng-Sheng 2008 でaspect ratioを保ったDMRGの計算が J/20, Yan-Huse-White, Depenbrock-McCulloch-Schollwock [cylinder DMRG] らが J/10程度, He-Zaletel-Oshikawa-Pollmann[cylinder DMRG + boundary shift] gapless などがあります. とくにYanらの2011年のScienceの仕事は 数値計算で ここまで根性を出せば何かできるかもしれない と多くの人に思わせた仕事でした. その後 tensor DMRGの発展と呼応して cylinder全盛となってしまった数値計算業界に対する 私たち [Nishimoto-Shibata-Hotta 2013] の立場/主張としては, cylinderの結果は 系の aspect ratioが1からすごく離れていて 本来のbulk系に適用するには 間違った結論に陥るというものです. 論文の supplementaryに実際, その事実を実証として載せてあります. この論文でaspect ratioを保った本計算では gapはJ/20 以下であるという結論を出しています.
最近 別途, 磁化率を計算してみましたが [Hotta-Asano, PRB 98 140405(R) (2018)] その結果だともっとgapが小さく見えてしまいます. さらに Tao Xiang (tensor) や Frederico Becca(VMC) などヨーロッパや中国の盟友たちは gaplessであるといっています. では本当はどう思うかと言われたら わからない, それくらいわからず たぶんただの数値計算精度競争をしても結論が出ない問題なんだろうと思います. そこで大事なことは 既存の仕事の劣化版や多少の精度改善版ではなく それまでやっていなかった視点や方法で 仕事をまたひとつ加えていくことです(Tao Xiangの仕事がよき例).
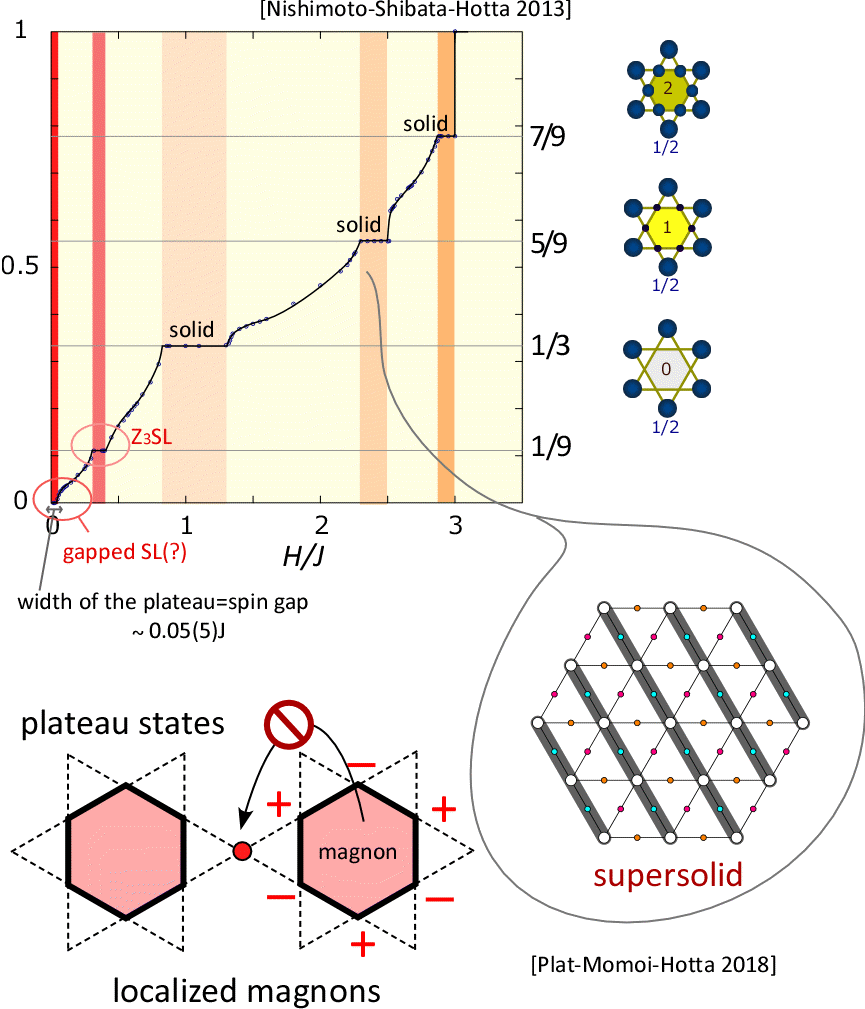
磁場下のkagome
一方 磁化過程については 図の最終結論といえる結果を出せていると思います [Nishimoto-Shibata-Hotta Nature Comm. 42287, 2013]. 基底状態を含む5つのプラトーがあり, 1/3, 5/9, 7/9はマグノンが系の並進対称性をやぶった スピン固体, 1/9は不思議なZ3スピン液体であると考えられます(topological項= ln 3). その後, この磁化過程はOkubo, Orusらのtensor networkの方法でも矛盾がない形で検証していただいています. 1/3, 5/9, 7/9は系が並進対称性をやぶってgapを生じる典型的なプラトーです: star of david の形の9格子点が状態のユニットとなっており, 中心にある六角形に マグノンが各々のプラトーで0/1/2個局在した状態が形成されています. マグノンが動かなくなった状態を「固体」とみなすことができ マグノンのoff diagonalな要素がnonzeroでプラトー間を滑らかに増加する磁化曲線内は 「液体」状態, 俗にいうmagnon BECです. ただしスピン液体直近の液体状態はその限りではありません.
その後, 理研のMomoiさんが主導して行った研究では 5/9 プラトー直下にsupersolidが出うるという結果が 得られました [Plat-Momoi-Hotta PRB 98, 014415 (2018)]. これは kinetic frustration 効果というkagomeの別の側面を顕にしたものです. kinetic frustrationとは何か?一言でいうとmagnonのhoppingの干渉効果であり, flat band ferromagnetismや Shastley Sutherland模型のmagnon localization を 引き起こしたのと同じ効果です. 上述のように 籠目のスピン固体プラトーには, 六角形のリングにマグノンが局在した状態ができます. 多くの場合 その波動関数は +/-/+/-/+/-のように大きさが逆で符号が異なるウェイトを持っています. このときリングにそって隣接した2つの格子点からリングの外の点にマグノンがhopしようとすると 逆符号で 等しいweightの寄与が打ち消しあって(干渉)実効的にhopping=0になり, リングの外に飛び出すことができない局在状態を生じます. より高次のhoppingまで考えるとマグノンが遍歴することは可能ではあるのですが それでも同様の文脈で一定以上の干渉効果が効いて マグノンバンド幅が著しく狭まり, 結果として 相互作用が相対的に大きなフラストレートした強相関系となるのです. このような理由で, マグノンが格子の一部を遍歴し 別の一部では局在している supersolid(超固体)が実現する のではないかという提案を行いました.
Kagomeの励起spectrum
最近, 籠目のTPQ時間発展を用いて「厳密に」有限サイズにおける線形・非線形励起スペクトル [Im χ(q,ω)] を求めました [Endoh-Hotta-Shimizu PRL121 220601 (2018)]. (もともとこの論文は手法開発の論文です. 有限サイズ効果に関しては 他のタグをご覧ください.) すると線形応答領域(quench磁場がまだ小さい領域)で求めた低エネルギースペクトルにやや broad目の, しかし 波数にほとんどよらないピークが立つことがわかりました. 通常は波に依存する鋭いピークが見られるのに対して, これらは以下のことを示唆しています: Broadである=「spinon」があるかもしれない, 波数に依存しない=spinonが局在している. つまり有限サイズではあるもののこのスペクトルは籠目のspin liquid基底状態の特異性を拾っている可能性があると考えています. ちなみに スピン液体で許される低エネルギー励起はspinonであり, 測定量としてspin liquidのsmoking gunとなりうる唯一の量は spinon continuumと呼ばれる broadな励起スペクトルであると考えられています[Hanらの実験].
S=3/2 kagome
最近では S=3/2の籠目格子で 磁場下で予想外になかなか面白いことが起こることがわかりました(JPS2019S発表:論文はお待ちください).
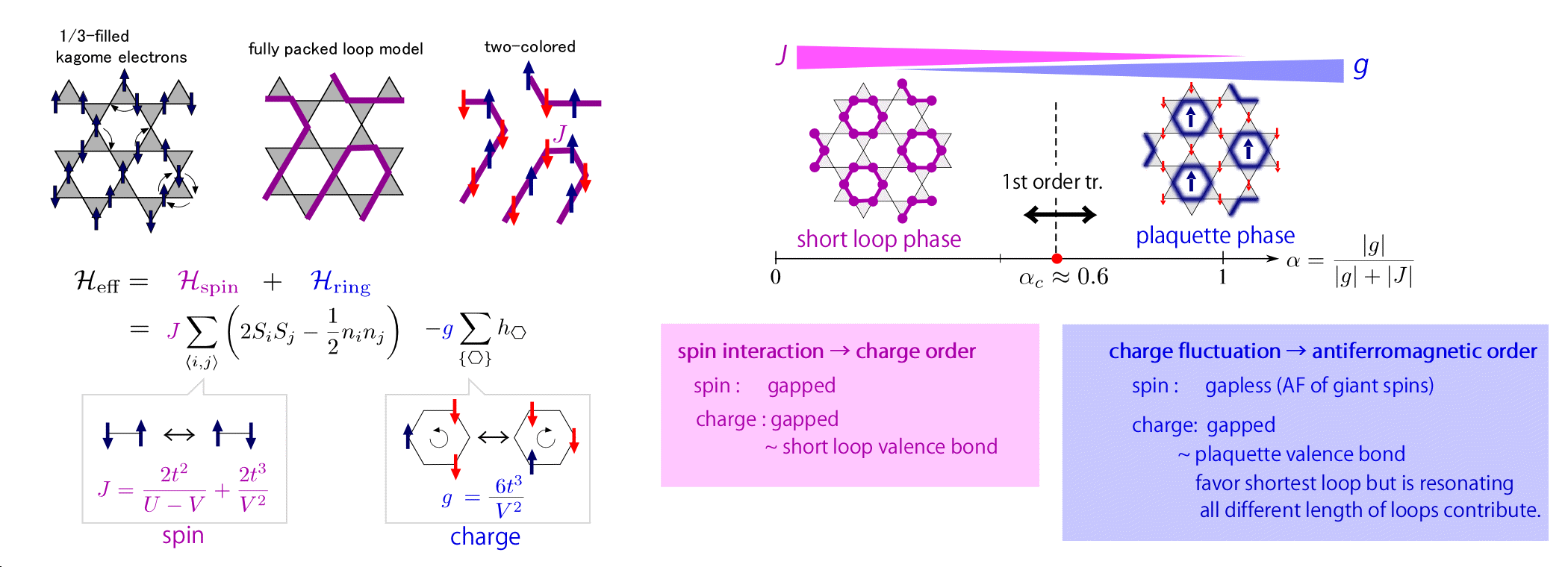
Kagome electrons
[Pollmann-Roychowdhury-Hotta-Penc, PRB 90 035118 (2014)].
相互作用が強い籠目格子上の相互作用する電子系は, 本当に複雑怪奇な低エネルギー構造を持っていることがわかりました. 電荷がhopしない強結合極限では, 1/3-filling (電荷の数が三角形当たり2個)のとき, 各三角形あたり(u d x) u=up ele, d=downele x=vacant という形で電子が配置しているあらゆるconfigurationが 系全体の hilbert spaceの半分を超える縮退を起こしています. ここにhoppingを摂動として加えたとき その揺らぎの効果は 2 colored fully packed loop modelというモデルの dynamicsとしてとらえることができるようになります. このloopは電子がいるサイトをつなぎ合わせて作られる仮想的なloopで, loopにそって電子のup/downのスピンを交互に 配置しています. いくつかの証明と数値計算によって スピンがこのloop状を電荷自由度とentangleしながら相互作用をして不思議な時期的な状態を作っていることがわかりました. 電荷のダイナミクス(ループの組み換え)を支配するgとheisenberg相互作用J の2パラメタの有効ハミルトニアンに簡単化されるのですが スピンの揺らぎが電荷を秩序化させ 電荷のゆらぎがスピンを秩序化させるという, 一見するとすぐわからないような物理が背後に潜んでいます.
(あとがき)これは今はすっかりbig nameになったFrank Pollmannが学生時代にやっていた仕事に関連して, 二人とも若かったころ 一緒に趣味でやり始めた仕事です. 途中からKarlo Pencも加わり大人の趣味と化し 7年かかりました. 大人の趣味だけあって 大変マニアックな研究ですが個人的には示唆的で気に入っています. 我々が講演, 紹介することは 今後ともないと思うのでここに記念にのせておきます. 裏話としては 最終局面で Arnaud Ralko が 相互作用が弱い状況で同じ問題を schwinger bosonであつかっていることがわかり やや大騒ぎに... 7年もだらだらやったからだ ! という話になり急に力を入れて研究をカンツイし出版しました. このあいだ Arnaudとこの話になり 盛り上がりました.