Tomonaga Luttinger Liquid in magnetic spin chains
In 1D, there is a class of quantum phase called Tomonaga-Luttinger liquid (TLL). The particular feature of this liquid is that its basic property is determined solely by the acoustic wave or a bosonic low energy excitation of many-body type. The thermodynamic properties are characterized a velocity v of this acoustic wave and a Tomonaga-Luttinger parameter K, which represents the effective interactions between the bosons. This holds regardless of the details of the system, what the degrees of freedom are (e.g. for electrons we consider two component TLL, and for magnets the single-component TLL). For example, if K exceeds some critical value, there is a phase transition breaking the discrete symmetry of the system. In the TLL, all the correlation functions behave critical and their exponents are determined by K's.
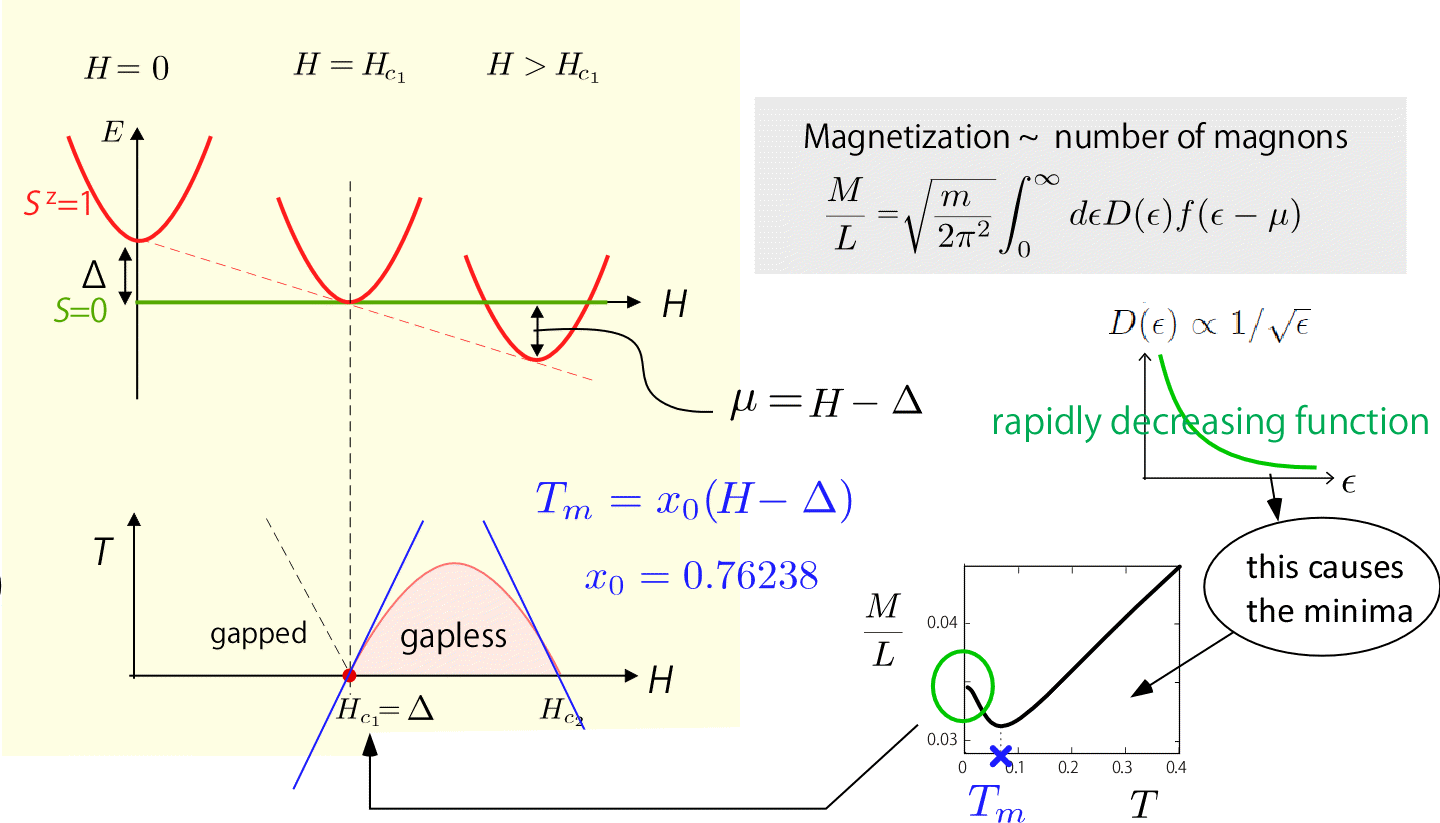
Now since this TLL does not break the symmetry of the system, there should be a crossover from the high temperature disordered/para phase to the TLL? How could we detect it? In our paper [Maeda-Hotta-Oshikawa, PRL 99 057205 (2007)] we showed that the crossover temperature can be determined from the local minima/maxima of the temperature dependence in the magnetization. In a spin gapped 1D magnet, e.g. Haldane chain, dimerized chain, spin ladders, the gap closes at the critical field Hc1, above which the Sz=1 magnons are doped successively. In 1D, this magnon phase is a TLL (in 2D or 3D it is a BEC). Just above Hc1, the number of magnons doped (=magnetization) is evaluated by the effective theory and the 1D density of states that diverges at the edge of the band contributes in such a way to give a minimum of magnetization as a function of temperature. We showed this both analytically and numerically, and after this study, this protocol is used frequently in experiments to determine the phase diagram of the gapped spin system.
Measuring TLL parameters in laboratories
[Hong, Kim, Hotta, Takano, Tremelling, Landee, Kang, Christensen, Schmidt, Lefmann, Uhrig, Broholm, PRL105, 137207 (2010)]
[Ninios, Hong, Manabe, Hotta, Herringer, Turnbull, Landee, Takano, Chan, PRL108 107201 (2012)]
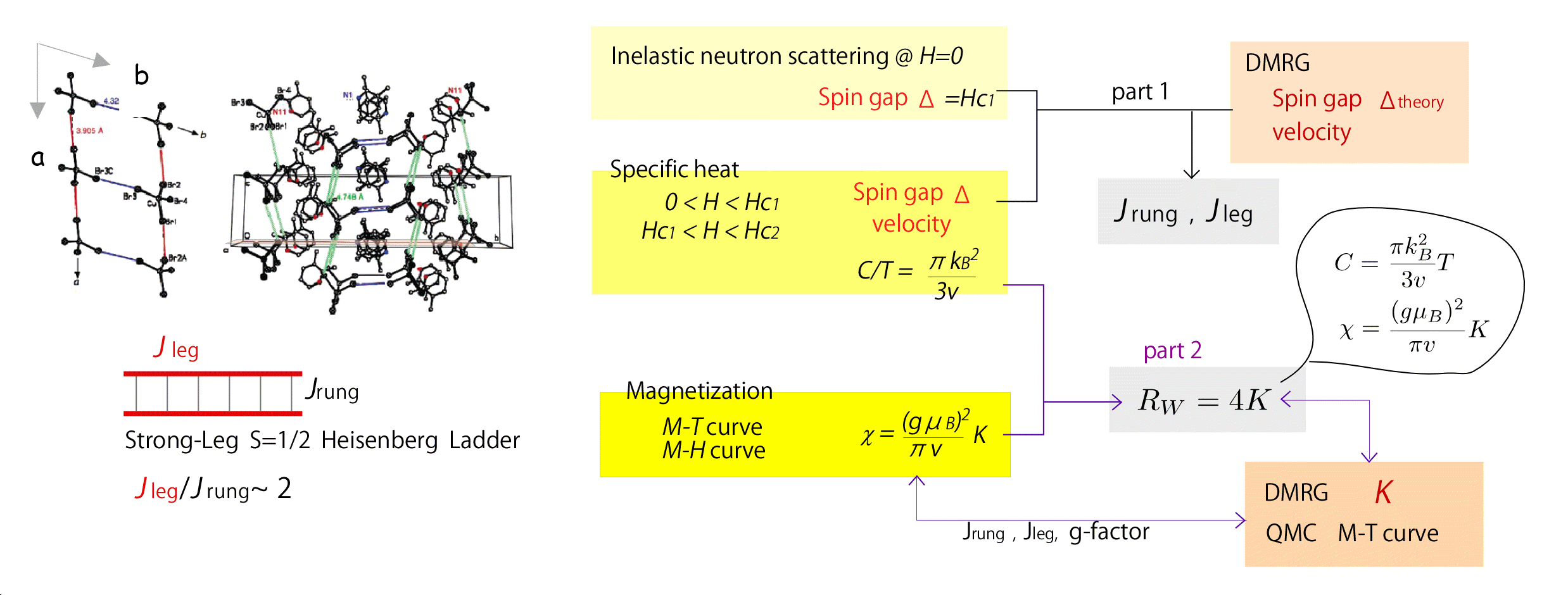
Unfortunately, there is not much examples of ideal 1D magnets in reality. One example is a spin ladder material DIMPY. Yasu Takano and collaborators worked with us to measure the TLL parameters in this material.
Part 1 :[Tao Hong et. al] the spin gap is evaluated from the specific heat measurement and from the neutron scattering experiment, and combined with DMRGm, we determined the model parameter J. Part2 [Ninios, et al.]; Based on the value of J determined experimentally, we calculated the TLL parameter K. Along with that, we found a universal relation between the so-called Wilson ratio RW, and the TL parameter K, which is RW=4K (pointed out for the first time). This Wilson ratio is based on the fact that for Fermi liquids, the specific heat behaves T-linear while the Pauli susceptibility is nearly constant, and by taking the ratio of the T-linear coefficients and susceptibility, one can derive a dimensionless parameter, which does not depend on the details the system. For noninteracting Fermi liquid RW=1 and for local Fermi liquid picture in a Kondo model, RW=2. Therefore, RW is usually considered as a measure of correlation in the system.
Going back to our TLL, we also have a T-linear specific heat and a constant χ, meaning that RW is being well defined.
We evaluated RW experimentally and compared with 4K derived from theoretical calculation.
Along with that, we compared the magnetization as functions of temperature in the experiment and from QMC calculation(by Manabe, our master student), and derived a phase diagram in a magnetic field by making use of our previous theory.
[Hong, Kim, Hotta, Takano, Tremelling, Landee, Kang, Christensen, Schmidt, Lefmann, Uhrig, Broholm, PRL105, 137207 (2010)]
[Ninios, Hong, Manabe, Hotta, Herringer, Turnbull, Landee, Takano, Chan, PRL108 107201 (2012)]
Unfortunately, there is not much examples of ideal 1D magnets in reality. One example is a spin ladder material DIMPY. Yasu Takano and collaborators worked with us to measure the TLL parameters in this material.
Part 1 :[Tao Hong et. al] the spin gap is evaluated from the specific heat measurement and from the neutron scattering experiment, and combined with DMRGm, we determined the model parameter J. Part2 [Ninios, et al.]; Based on the value of J determined experimentally, we calculated the TLL parameter K. Along with that, we found a universal relation between the so-called Wilson ratio RW, and the TL parameter K, which is RW=4K (pointed out for the first time). This Wilson ratio is based on the fact that for Fermi liquids, the specific heat behaves T-linear while the Pauli susceptibility is nearly constant, and by taking the ratio of the T-linear coefficients and susceptibility, one can derive a dimensionless parameter, which does not depend on the details the system. For noninteracting Fermi liquid RW=1 and for local Fermi liquid picture in a Kondo model, RW=2. Therefore, RW is usually considered as a measure of correlation in the system.
Going back to our TLL, we also have a T-linear specific heat and a constant χ, meaning that RW is being well defined.
We evaluated RW experimentally and compared with 4K derived from theoretical calculation.
Along with that, we compared the magnetization as functions of temperature in the experiment and from QMC calculation(by Manabe, our master student), and derived a phase diagram in a magnetic field by making use of our previous theory.

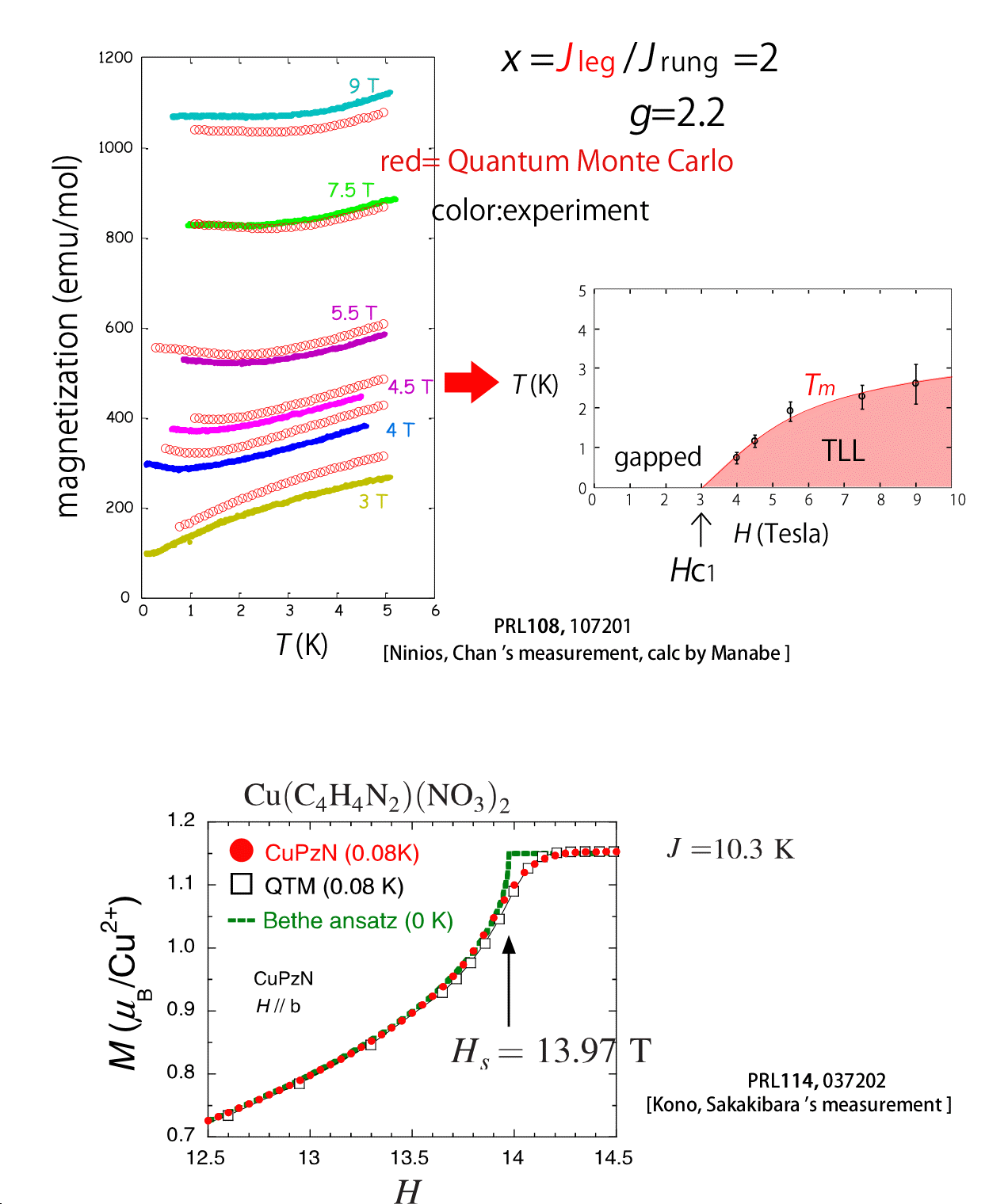
We finally briefly introduce the work by Yohei Kohno in ISSP(phD thesis)
on the ideal spin-1/2 Heisenberg chain material, CuPZN
[Kono, Sakakibara, et.al. PRL 114 037202 (2015)] .
Surprizingly, the magnetization of this material shows almost exact coincidence with the theoretical exact solution we calculated by using a quantum transfer matrix method (red circles versus square). The critical phenomena near the saturation field are also very clear. The work demonstrates the critical phenomena of the 1D quantum Heisenberg model for the first time in laboratories.
Surprizingly, the magnetization of this material shows almost exact coincidence with the theoretical exact solution we calculated by using a quantum transfer matrix method (red circles versus square). The critical phenomena near the saturation field are also very clear. The work demonstrates the critical phenomena of the 1D quantum Heisenberg model for the first time in laboratories.