Tomonaga Luttinger Liquid in magnetic spin chains
量子ゆらぎは低次元ほど発達します. 特に一次元系では低温で朝永ラッティンジャー液体(TLL)と呼ばれる特別な量子多体状態が実現します. TLLにおいては 系がある種の音波の自由度だけで記述され, 音波の伝播速度vと朝永ラッティンジャーパラメタ K という二つの普遍的パラメタだけで あらゆる熱力学的性質が決まります. ここで音波というのは ボソンであらわされる多体励起です. k=0から出て広がるdes Cloizeaux-Pearson modeの直上の連続励起がそれにあたり, この多体励起しか許されないのが1次元系ならではの特質です. Kは 有効的な相互作用定数とみなすことができ, 「Kがある閾値を超えると液体から固体への相転移が起こる」, 「TLLのあらゆる2体相関関数がべき的にふるまい, そのべきがKで決まる」, などTLLについては理論的にはほぼすべての性質が古くからわかっています. このことは系の詳細に一切拠らないため, 電子系でもスピン系でも同様の扱いができます. そして1次元の量子磁性体はsingle componentのTLLをなします.
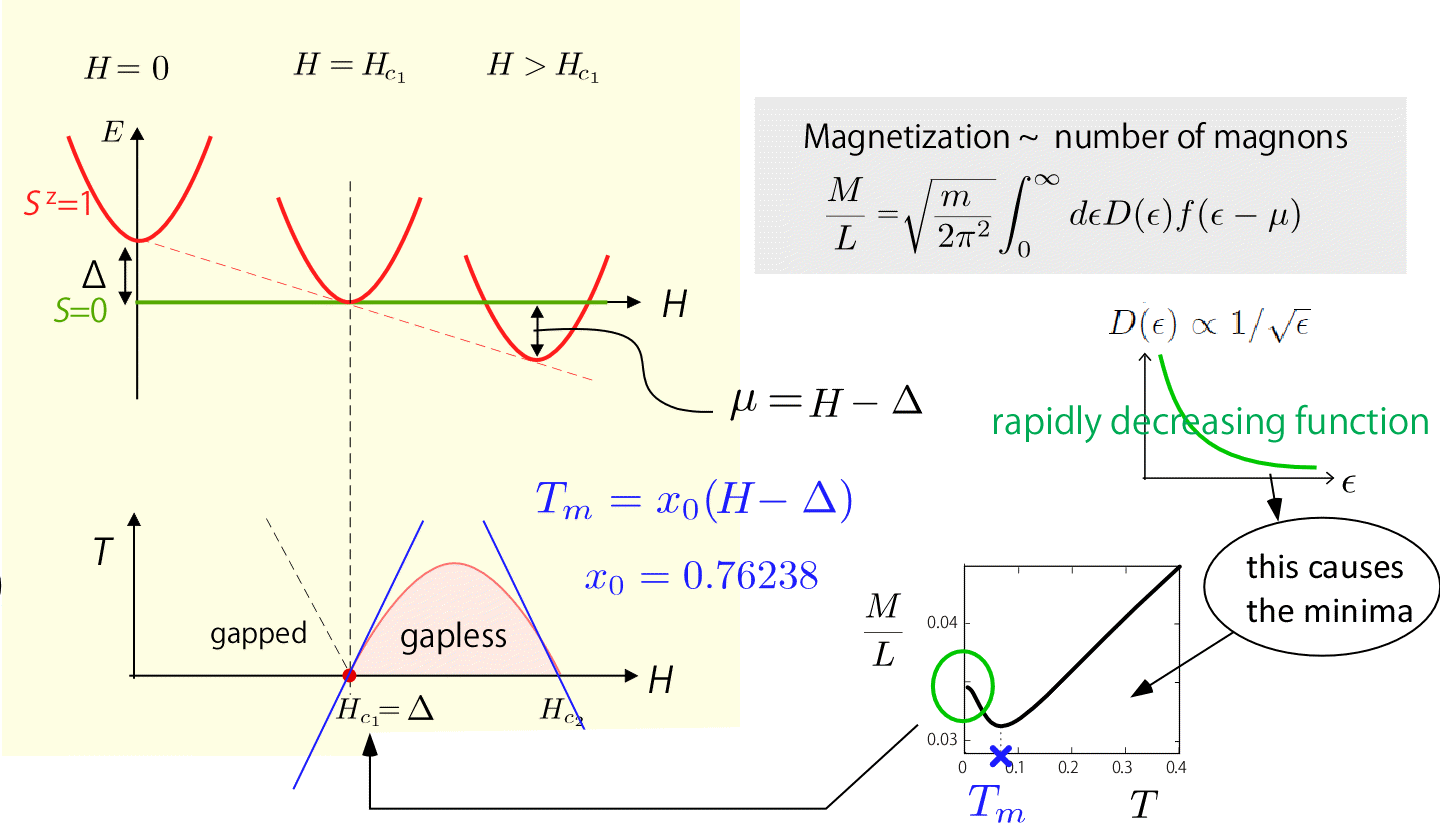
しかしそもそもどの温度で 高温のparamagnetから低温のTLLへと変化するのか? そのクロスオーバー温度は 磁化率から出せることがわかりました [Maeda-Hotta-Oshikawa, PRL 99 057205 (2007)] ( PRBに投稿してPRLにtransferされた伝説の仕事です). スピンギャップのある1次元磁性体(たとえば Haldane鎖)に磁場をかけると ギャップが閉じる磁場の値Hc1からマグノンが dopeされ TLLとなります. ギャップが閉じた磁場近傍では, 磁化が1次元の状態密度の関数形を反映し, ある温度で極小値を示します. これがTLLのonsetを支配する温度であることを低エネルギー有効理論と数値計算で示したものです. この理論によって実験系で磁化測定から 具体的に温度-磁場相図がかけるようになりました. TLL相の立ち上がりの傾きは系の詳細によらない universalな値を示します.
実験と理論のcollab
[Hong, Kim, Hotta, Takano, Tremelling, Landee, Kang, Christensen, Schmidt, Lefmann, Uhrig, Broholm, PRL105, 137207 (2010)]
[Ninios, Hong, Manabe, Hotta, Herringer, Turnbull, Landee, Takano, Chan, PRL108 107201 (2012)]
しかし理想的な1次元系はなかなかありません. そのような中で gapがある spin ladder物質 DIMPYに対して 行ったあるひとまとまりの仕事(Yasu Takano project)を簡単にご紹介します.
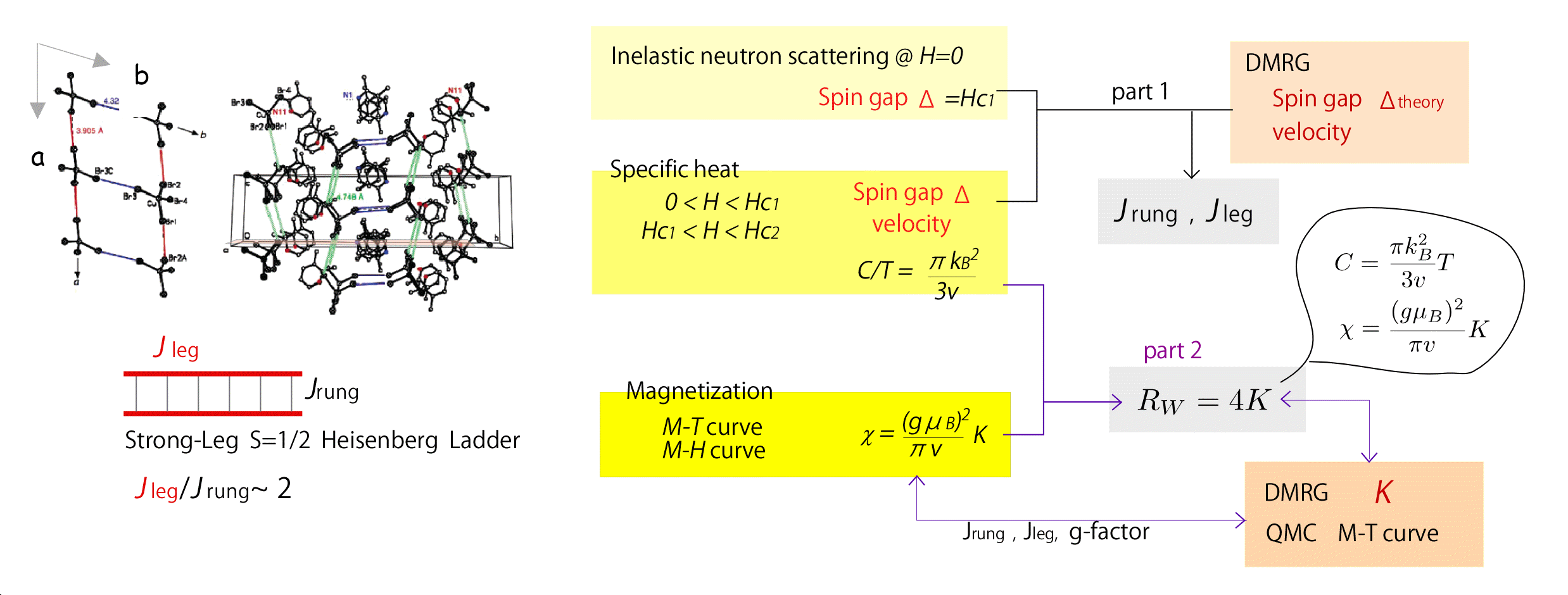
Part 1 [Tao Hong et. al] では, 比熱と中性子からはかったspin gapが DMRG計算におけるギャップと整合するように モデルパラメタJを同定しました. Part2 [Ninios, et al.] では 実験から得られたmodel parameter Jをもとにして行ったDMRG計算から得た TLパラメタKと, 磁化率及び比熱から得た Wilson比 Rwが 理論的に満たすべき Rw=4Kという対応関係にあることを示しました. Wilson比はもともと Fermi液体論でT-linearな低温比熱の 比例係数とPauli磁化率(定数)の比として 与えられる無次元量です(系の詳細によらない). 相関がない Fermi液体では Rw=1, 近藤系のような局所Fermi液体は Rw=2である ことから相互作用の強さの指標となっていました. しかしよく考えれば Fermi液体とは 本来全く違うタイプの量子液体であるはずの 1次元のTLLでも T-linearな低温比熱と磁化率一定の振る舞いが得られます. そしてその比は Rw=4Kとなることをこの論文がおそらく初めて指摘しているはずです.
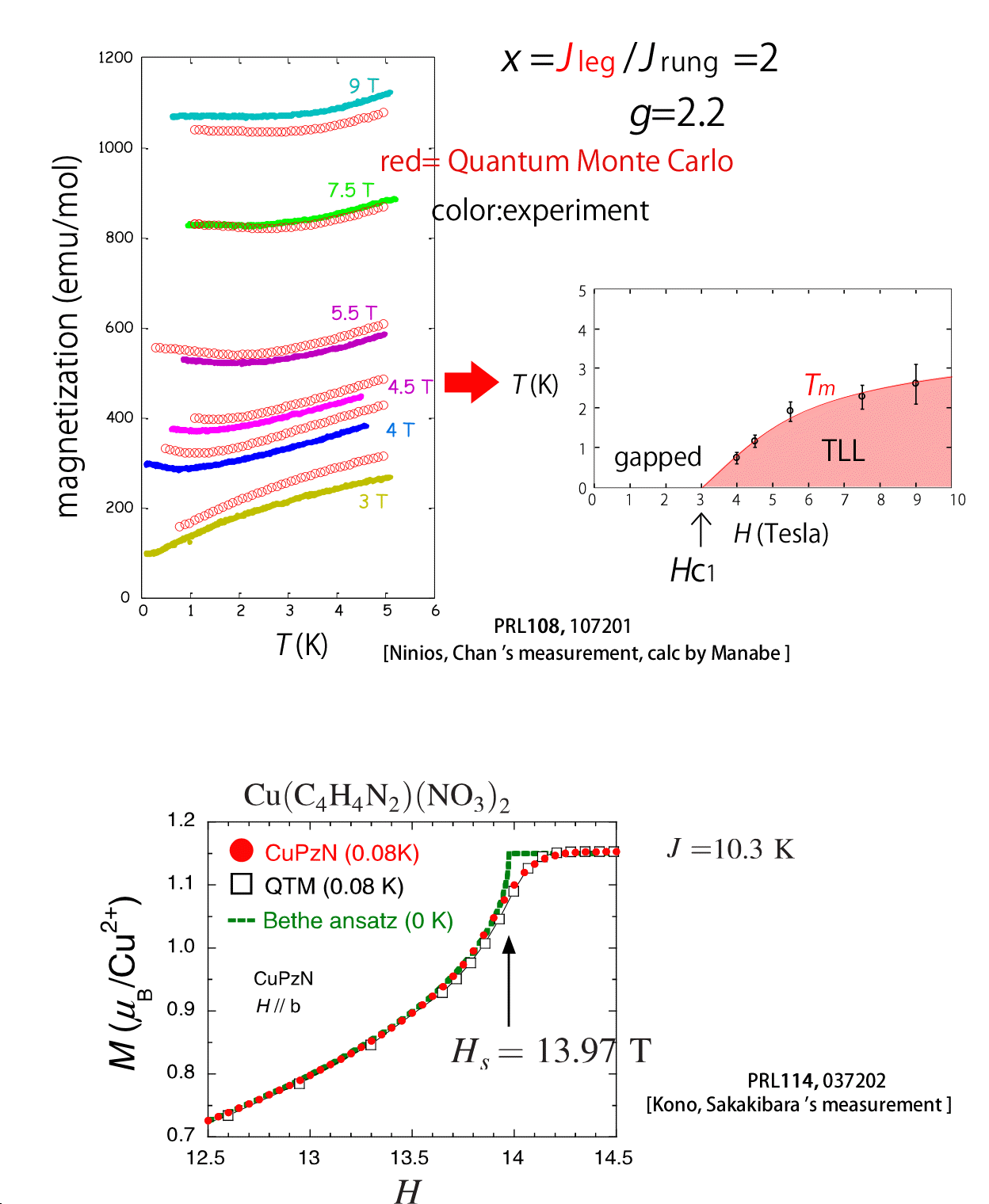
この系ではManabeくん(KSUにおける修士)にQMCで磁化率を計算してもらい, 磁化率の極小値から相図を出すこともできました.
[Hong, Kim, Hotta, Takano, Tremelling, Landee, Kang, Christensen, Schmidt, Lefmann, Uhrig, Broholm, PRL105, 137207 (2010)]
[Ninios, Hong, Manabe, Hotta, Herringer, Turnbull, Landee, Takano, Chan, PRL108 107201 (2012)]
しかし理想的な1次元系はなかなかありません. そのような中で gapがある spin ladder物質 DIMPYに対して 行ったあるひとまとまりの仕事(Yasu Takano project)を簡単にご紹介します.
Part 1 [Tao Hong et. al] では, 比熱と中性子からはかったspin gapが DMRG計算におけるギャップと整合するように モデルパラメタJを同定しました. Part2 [Ninios, et al.] では 実験から得られたmodel parameter Jをもとにして行ったDMRG計算から得た TLパラメタKと, 磁化率及び比熱から得た Wilson比 Rwが 理論的に満たすべき Rw=4Kという対応関係にあることを示しました. Wilson比はもともと Fermi液体論でT-linearな低温比熱の 比例係数とPauli磁化率(定数)の比として 与えられる無次元量です(系の詳細によらない). 相関がない Fermi液体では Rw=1, 近藤系のような局所Fermi液体は Rw=2である ことから相互作用の強さの指標となっていました. しかしよく考えれば Fermi液体とは 本来全く違うタイプの量子液体であるはずの 1次元のTLLでも T-linearな低温比熱と磁化率一定の振る舞いが得られます. そしてその比は Rw=4Kとなることをこの論文がおそらく初めて指摘しているはずです.
この系ではManabeくん(KSUにおける修士)にQMCで磁化率を計算してもらい, 磁化率の極小値から相図を出すこともできました.

実験と理論をきれいに整合させて有意な結論を得ることはなかなか大変な作業であり
1次元量子スピンだから可能であったと思われます.
その後, 私が関わった一連の仕事の最後に 今度は S=1/2の理想的なスピン鎖物質CuPZN [Kono, Sakakibara, et.al. PRL 114 037202 (2015):河野氏@isspの博士論文] が あります. この物質の磁化過程は驚くべき精度で厳密解と一致します. たとえば図にある赤い測定点とQuantum transfer method(QTM) という有限温度で計算した厳密な値までが実に綺麗にあってしまうのです. 更に磁場をかけた際, saturation field付近の比熱の臨界指数まできれいに整合してしまうという物質でした. この仕事の位置づけは1次元の理想的なheisenberg modelの臨界現象を初めてlaboratoryでとらえたというものです.
これらの実験に共通するのは たとえば臨界磁場まで 15Tまでで届くような理想的1次元物質をさがしたり 低温で有意な比熱を測れるように deutrationが可能な物質をうまく探し出して projectを設計する眼, そしてどのような測定をすればすべての整合性が検証できるか? を考える緻密さが, 実験の背後にあるところです.
これらはいわゆる荒野をゆく冒険的な仕事とは違いますが, 実に教科書的でいわゆる美しい実験の仕事だと思います. やはり実験の測定量があって検証してこその「universalな理論」 であるということをよく示しています.
その後, 私が関わった一連の仕事の最後に 今度は S=1/2の理想的なスピン鎖物質CuPZN [Kono, Sakakibara, et.al. PRL 114 037202 (2015):河野氏@isspの博士論文] が あります. この物質の磁化過程は驚くべき精度で厳密解と一致します. たとえば図にある赤い測定点とQuantum transfer method(QTM) という有限温度で計算した厳密な値までが実に綺麗にあってしまうのです. 更に磁場をかけた際, saturation field付近の比熱の臨界指数まできれいに整合してしまうという物質でした. この仕事の位置づけは1次元の理想的なheisenberg modelの臨界現象を初めてlaboratoryでとらえたというものです.
これらの実験に共通するのは たとえば臨界磁場まで 15Tまでで届くような理想的1次元物質をさがしたり 低温で有意な比熱を測れるように deutrationが可能な物質をうまく探し出して projectを設計する眼, そしてどのような測定をすればすべての整合性が検証できるか? を考える緻密さが, 実験の背後にあるところです.
これらはいわゆる荒野をゆく冒険的な仕事とは違いますが, 実に教科書的でいわゆる美しい実験の仕事だと思います. やはり実験の測定量があって検証してこその「universalな理論」 であるということをよく示しています.